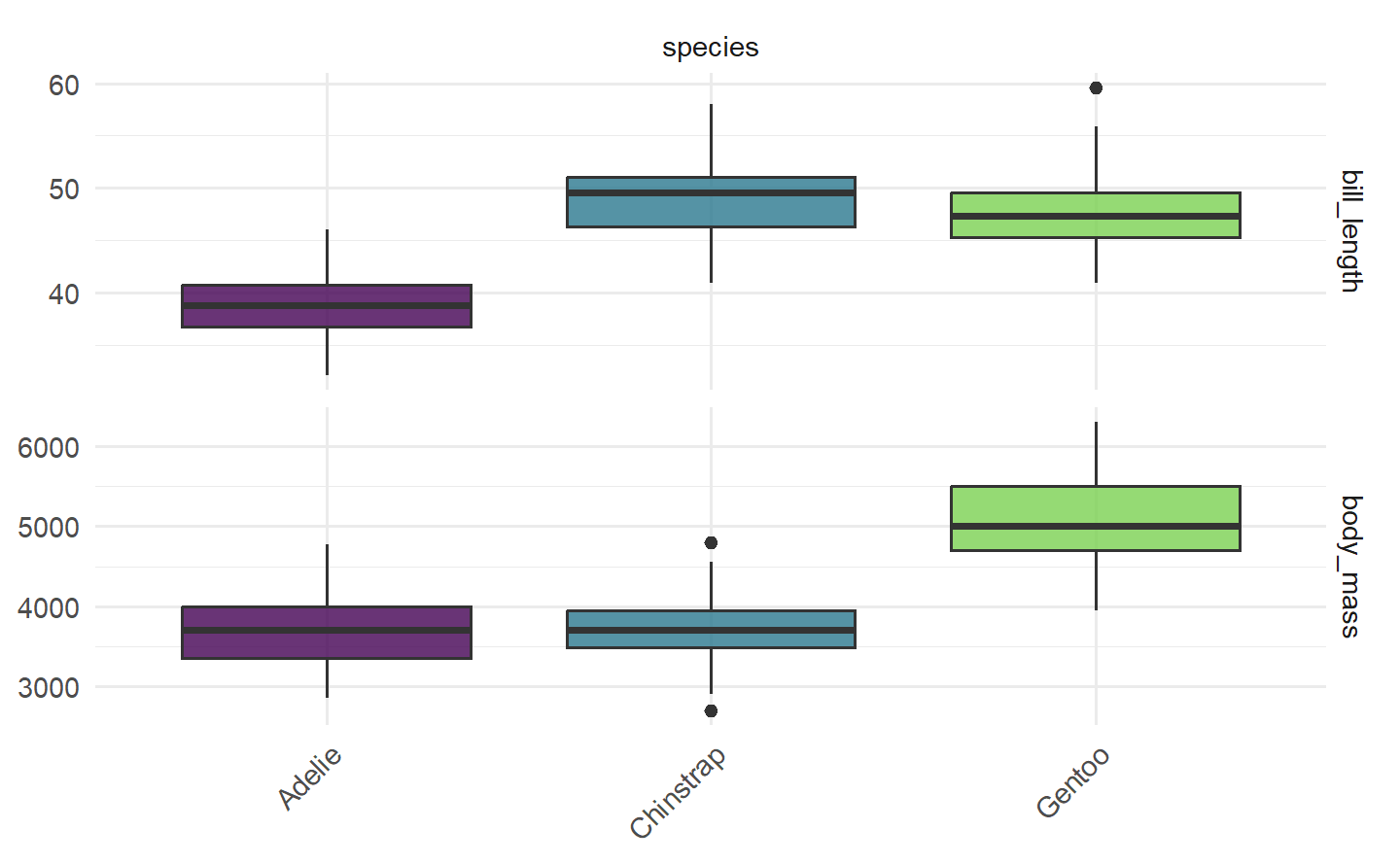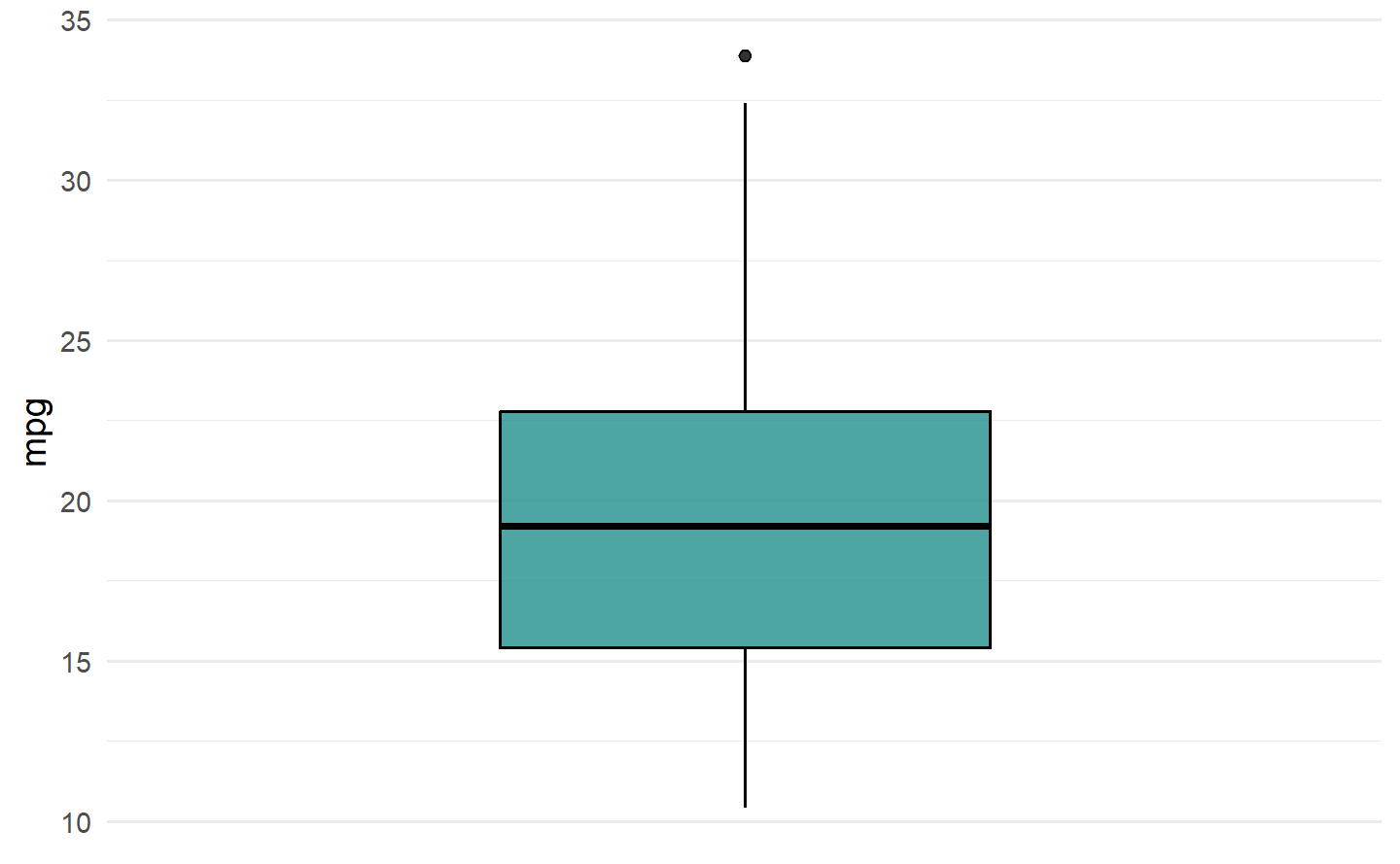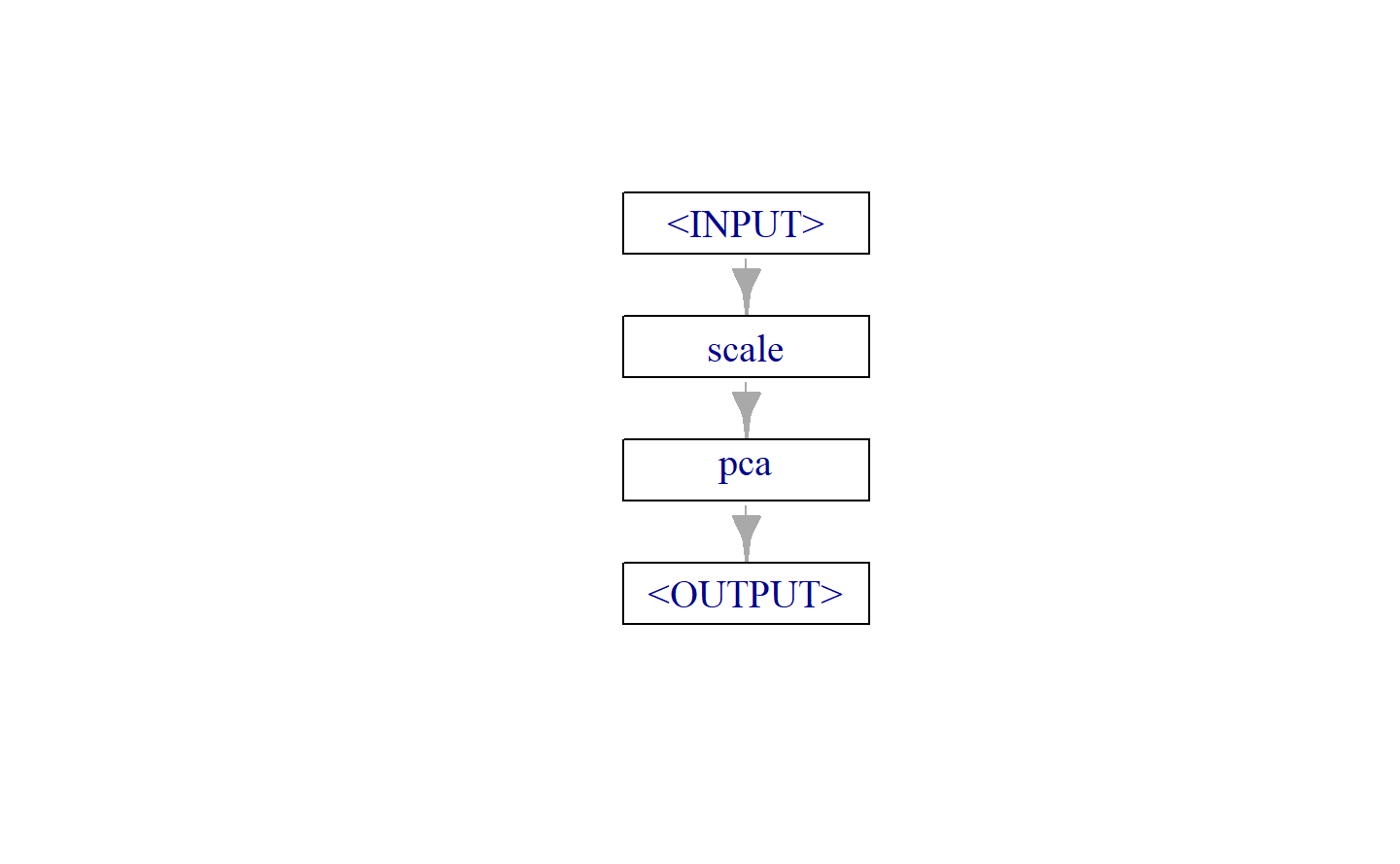Progress

Learning Progress: Completed.🥳

Learning Source

张敬信老师 QQ 群（222427909）文件
https://github.com/zhjx19/RConf15/tree/main

library(mlr3verse)

1 基础知识

1.1 任务：封装数据

任务是表格数据的封装，自变量为特征，因变量为目标或结果变量。

tsks() # 查看所有自带任务
#> <DictionaryTask> with 21 stored values
#> Keys: ames_housing, bike_sharing, boston_housing, breast_cancer,
#>   german_credit, ilpd, iris, kc_housing, moneyball, mtcars, optdigits,
#>   penguins, penguins_simple, pima, ruspini, sonar, spam, titanic,
#>   usarrests, wine, zoo

# 创建任务
dat = tsk("german_credit")$data() # 提取数据
task = as_task_classif(dat, target = "credit_risk")
task
#> <TaskClassif:dat> (1000 x 21)
#> * Target: credit_risk
#> * Properties: twoclass
#> * Features (20):
#>   - fct (14): credit_history, employment_duration, foreign_worker,
#>     housing, job, other_debtors, other_installment_plans,
#>     people_liable, personal_status_sex, property, purpose, savings,
#>     status, telephone
#>   - int (3): age, amount, duration
#>   - ord (3): installment_rate, number_credits, present_residence

# 选择特征
task$select(cols = setdiff(task$feature_names, "telephone"))
task
#> <TaskClassif:dat> (1000 x 20)
#> * Target: credit_risk
#> * Properties: twoclass
#> * Features (19):
#>   - fct (13): credit_history, employment_duration, foreign_worker,
#>     housing, job, other_debtors, other_installment_plans,
#>     people_liable, personal_status_sex, property, purpose, savings,
#>     status
#>   - int (3): age, amount, duration
#>   - ord (3): installment_rate, number_credits, present_residence

# 划分训练集、测试集
set.seed(1)
split = partition(task, ratio = .7)

stratify = TRUE 默认按目标变量分层，得到训练集和测试集的索引（行号）。

1.2 学习器：封装算法

lrns()  # 查看所有自带学习器名字
#> <DictionaryLearner> with 46 stored values
#> Keys: classif.cv_glmnet, classif.debug, classif.featureless,
#>   classif.glmnet, classif.kknn, classif.lda, classif.log_reg,
#>   classif.multinom, classif.naive_bayes, classif.nnet, classif.qda,
#>   classif.ranger, classif.rpart, classif.svm, classif.xgboost,
#>   clust.agnes, clust.ap, clust.cmeans, clust.cobweb, clust.dbscan,
#>   clust.diana, clust.em, clust.fanny, clust.featureless, clust.ff,
#>   clust.hclust, clust.kkmeans, clust.kmeans, clust.MBatchKMeans,
#>   clust.mclust, clust.meanshift, clust.pam, clust.SimpleKMeans,
#>   clust.xmeans, regr.cv_glmnet, regr.debug, regr.featureless,
#>   regr.glmnet, regr.kknn, regr.km, regr.lm, regr.nnet, regr.ranger,
#>   regr.rpart, regr.svm, regr.xgboost

# 选择随机森林分类学习器
learner = lrn("classif.ranger", num.trees = 100, predict_type = "prob")
learner
#> <LearnerClassifRanger:classif.ranger>
#> * Model: -
#> * Parameters: num.threads=1, num.trees=100
#> * Packages: mlr3, mlr3learners, ranger
#> * Predict Types:  response, [prob]
#> * Feature Types: logical, integer, numeric, character, factor, ordered
#> * Properties: hotstart_backward, importance, multiclass, oob_error,
#>   twoclass, weights

学习器 $model 属性为 NULL，用 $train() 方法在训练集上训练模型，模型结果存入 $model，再用 predict() 方法在测试集上做预测，得到结果是 Prediction 对象。

learner$train(task, row_ids = split$train)
learner$model
#> Ranger result
#> 
#> Call:
#>  ranger::ranger(dependent.variable.name = task$target_names, data = task$data(),      probability = self$predict_type == "prob", case.weights = task$weights$weight,      num.threads = 1L, num.trees = 100L) 
#> 
#> Type:                             Probability estimation 
#> Number of trees:                  100 
#> Sample size:                      700 
#> Number of independent variables:  19 
#> Mtry:                             4 
#> Target node size:                 10 
#> Variable importance mode:         none 
#> Splitrule:                        gini 
#> OOB prediction error (Brier s.):  0.1615879

prediction = learner$predict(task, row_ids = split$test)
prediction

1.3 性能评估

msrs() # 查看所有支持的性能度量指标
#> <DictionaryMeasure> with 66 stored values
#> Keys: aic, bic, classif.acc, classif.auc, classif.bacc, classif.bbrier,
#>   classif.ce, classif.costs, classif.dor, classif.fbeta, classif.fdr,
#>   classif.fn, classif.fnr, classif.fomr, classif.fp, classif.fpr,
#>   classif.logloss, classif.mauc_au1p, classif.mauc_au1u,
#>   classif.mauc_aunp, classif.mauc_aunu, classif.mbrier, classif.mcc,
#>   classif.npv, classif.ppv, classif.prauc, classif.precision,
#>   classif.recall, classif.sensitivity, classif.specificity, classif.tn,
#>   classif.tnr, classif.tp, classif.tpr, clust.ch, clust.dunn,
#>   clust.silhouette, clust.wss, debug_classif, oob_error, regr.bias,
#>   regr.ktau, regr.mae, regr.mape, regr.maxae, regr.medae, regr.medse,
#>   regr.mse, regr.msle, regr.pbias, regr.rae, regr.rmse, regr.rmsle,
#>   regr.rrse, regr.rse, regr.rsq, regr.sae, regr.smape, regr.srho,
#>   regr.sse, selected_features, sim.jaccard, sim.phi, time_both,
#>   time_predict, time_train

用预测对象的 $score() 方法，计算该度量指标的得分：

prediction$score(msr("classif.acc"))  # 准确率

# 绘制 ROC 曲线
library(precrec)
autoplot(prediction, type = "roc")

prediction$score(msr("classif.auc"))  # auc 面积

1.4 重抽样

rsmps()  # 查看所有支持的重抽样方法
#> <DictionaryResampling> with 9 stored values
#> Keys: bootstrap, custom, custom_cv, cv, holdout, insample, loo,
#>   repeated_cv, subsampling

cv10 = rsmp("cv", folds = 10)  # 10 折交叉验证

1.4.1 实例化重抽样对象

cv10$instantiate(task)  # 实例化
cv10$iters  # 数据副本数
#> [1] 10

cv10$train_set(1)  # 第 1 个数据副本的训练集索引
cv10$test_set(1)   # 第 1 个数据副本的测试集索引

1.4.2 使用重抽样

rr =  resample(task, learner, cv10, store_models = TRUE)
#> INFO  [16:41:32.671] [mlr3] Applying learner 'classif.ranger' on task 'dat' (iter 1/10)
#> INFO  [16:41:32.935] [mlr3] Applying learner 'classif.ranger' on task 'dat' (iter 2/10)
#> INFO  [16:41:32.995] [mlr3] Applying learner 'classif.ranger' on task 'dat' (iter 3/10)
#> INFO  [16:41:33.051] [mlr3] Applying learner 'classif.ranger' on task 'dat' (iter 4/10)
#> INFO  [16:41:33.107] [mlr3] Applying learner 'classif.ranger' on task 'dat' (iter 5/10)
#> INFO  [16:41:33.167] [mlr3] Applying learner 'classif.ranger' on task 'dat' (iter 6/10)
#> INFO  [16:41:33.226] [mlr3] Applying learner 'classif.ranger' on task 'dat' (iter 7/10)
#> INFO  [16:41:33.281] [mlr3] Applying learner 'classif.ranger' on task 'dat' (iter 8/10)
#> INFO  [16:41:33.338] [mlr3] Applying learner 'classif.ranger' on task 'dat' (iter 9/10)
#> INFO  [16:41:33.395] [mlr3] Applying learner 'classif.ranger' on task 'dat' (iter 10/10)

rr$aggregate(msr("classif.acc"))  # 所有重抽样的平均准确率
#> classif.acc 
#>       0.753

rr$score(msr("classif.acc"))  # 各个重抽样的平均准确率
#>     task_id     learner_id resampling_id iteration classif.acc
#>  1:     dat classif.ranger            cv         1        0.77
#>  2:     dat classif.ranger            cv         2        0.84
#>  3:     dat classif.ranger            cv         3        0.70
#>  4:     dat classif.ranger            cv         4        0.77
#>  5:     dat classif.ranger            cv         5        0.76
#>  6:     dat classif.ranger            cv         6        0.75
#>  7:     dat classif.ranger            cv         7        0.71
#>  8:     dat classif.ranger            cv         8        0.83
#>  9:     dat classif.ranger            cv         9        0.66
#> 10:     dat classif.ranger            cv        10        0.74
#> Hidden columns: task, learner, resampling, prediction

# 查看第 1 个数据副本（第 1 折）上的结果
rr$resampling$train_set(1)  # 第 1 折的训练集索引
rr$learners[[1]]$model      # 第 1 折学习器的拟合模型
rr$predictions()[[1]]       # 第 1 折的预测结果

1.5 基准测试

基准测试（benchmark）用来比较不同学习器（算法）、在多个任务（数据）和/或不同重抽样策略（多个数据副本）上的平均性能表现。

基准测试时有个关键问题：测试的公平性。即每个算法的每次测试必须在相同的重抽样训练集拟合模型，在相同的重抽样测试集评估性能。这些事情 beachmark() 会自动做好。

tasks = tsk("sonar")  # 可以多任务
learners = lrns(c("classif.rpart", "classif.kknn", "classif.ranger", "classif.svm"),
                predict_type = "prob")
design = benchmark_grid(tasks, learners, rsmps("cv", folds = 5))
design
#>     task        learner resampling
#> 1: sonar  classif.rpart         cv
#> 2: sonar   classif.kknn         cv
#> 3: sonar classif.ranger         cv
#> 4: sonar    classif.svm         cv

bmr = benchmark(design)  # 执行基准测试
bmr$aggregate(list(msr("classif.acc"), msr("classif.auc")))  # 汇总基准测试结果

# 可视化：对比性能
autoplot(bmr, type = "roc")  # ROC 曲线
autoplot(bmr, measure = msr("classif.auc"))  # AUC 箱线图

1.6 可视化

mlr3viz 包定义了 autoplot() 函数来用 ggplot2 绘图。通常一个对象有不止一种类型的图，可以通过 type 参数来改变绘图。图形使用 viridis 的调色板，外观由 theme 参数控制，默认是 minimal 主题。

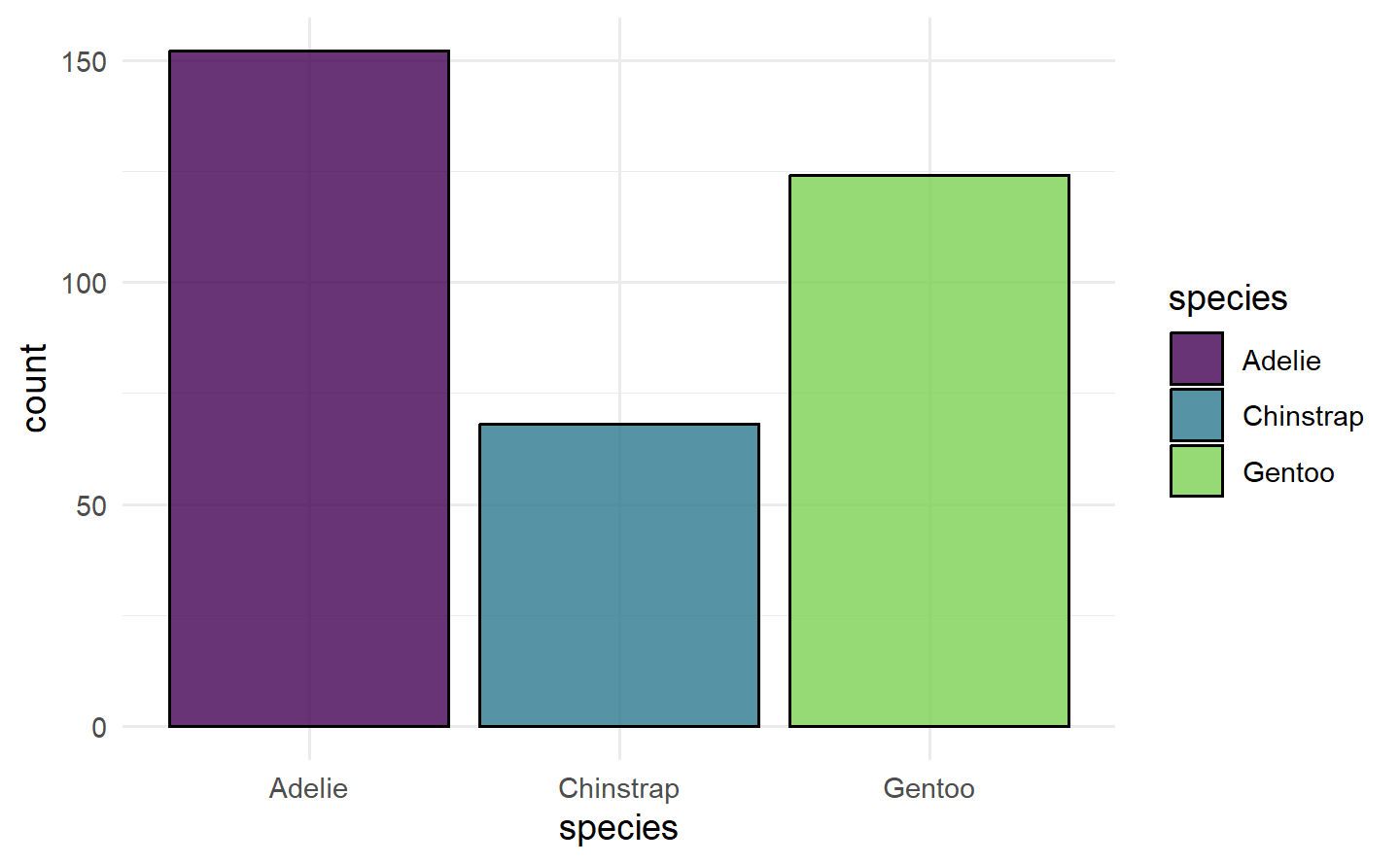
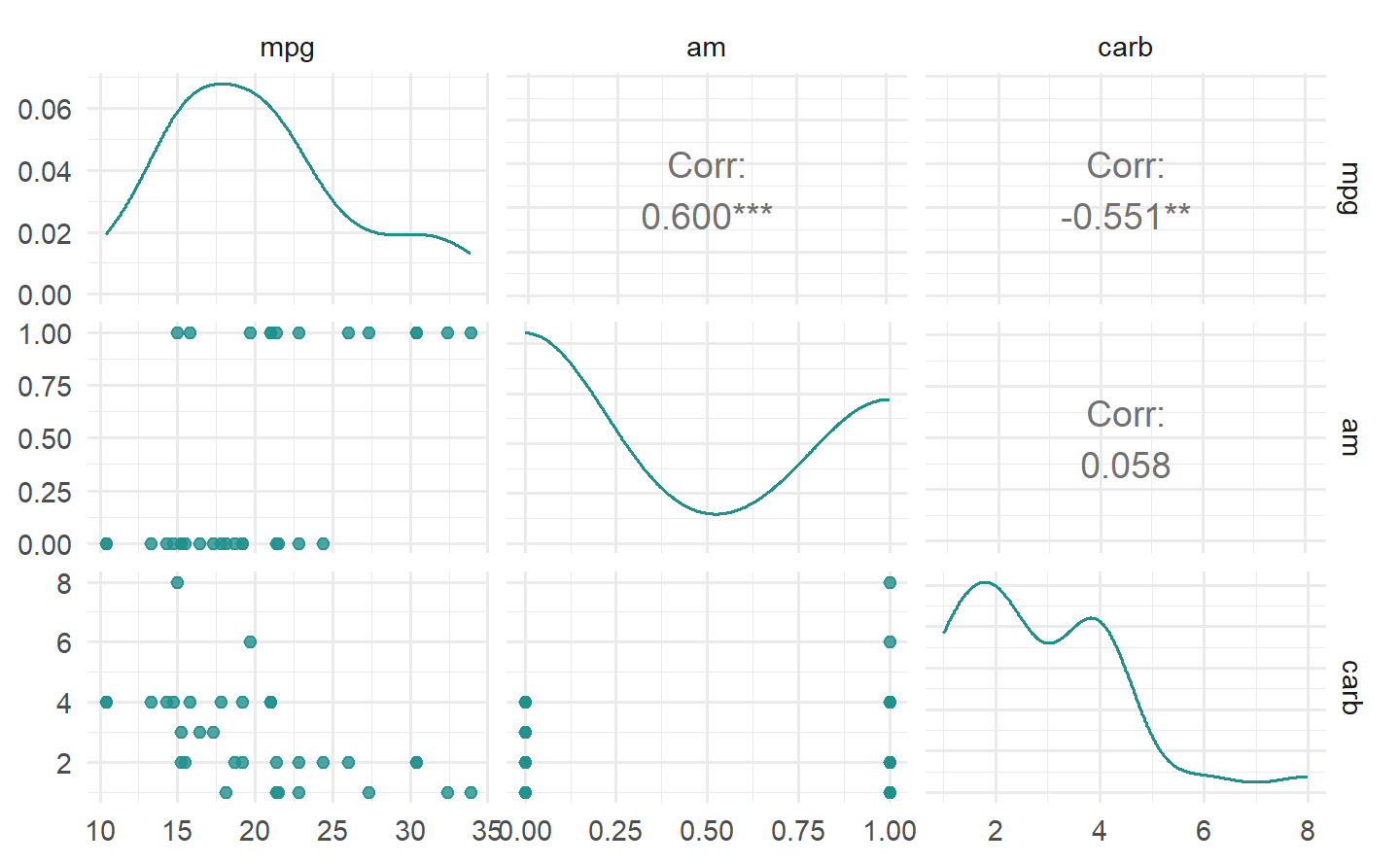
1.6.1 可视化任务

1.6.1.1 分类任务

task = tsk("penguins")
task$select(c("body_mass", "bill_length"))

autoplot(task, type = "target")  # "target" 图：条形图展示目标变量的各类别频数
autoplot(task, type = "duo")     # "duo" 图：箱线图展示多个特征的分布
autoplot(task, type = "pairs")   # "pairs" 图：展示多个特征的成对比较

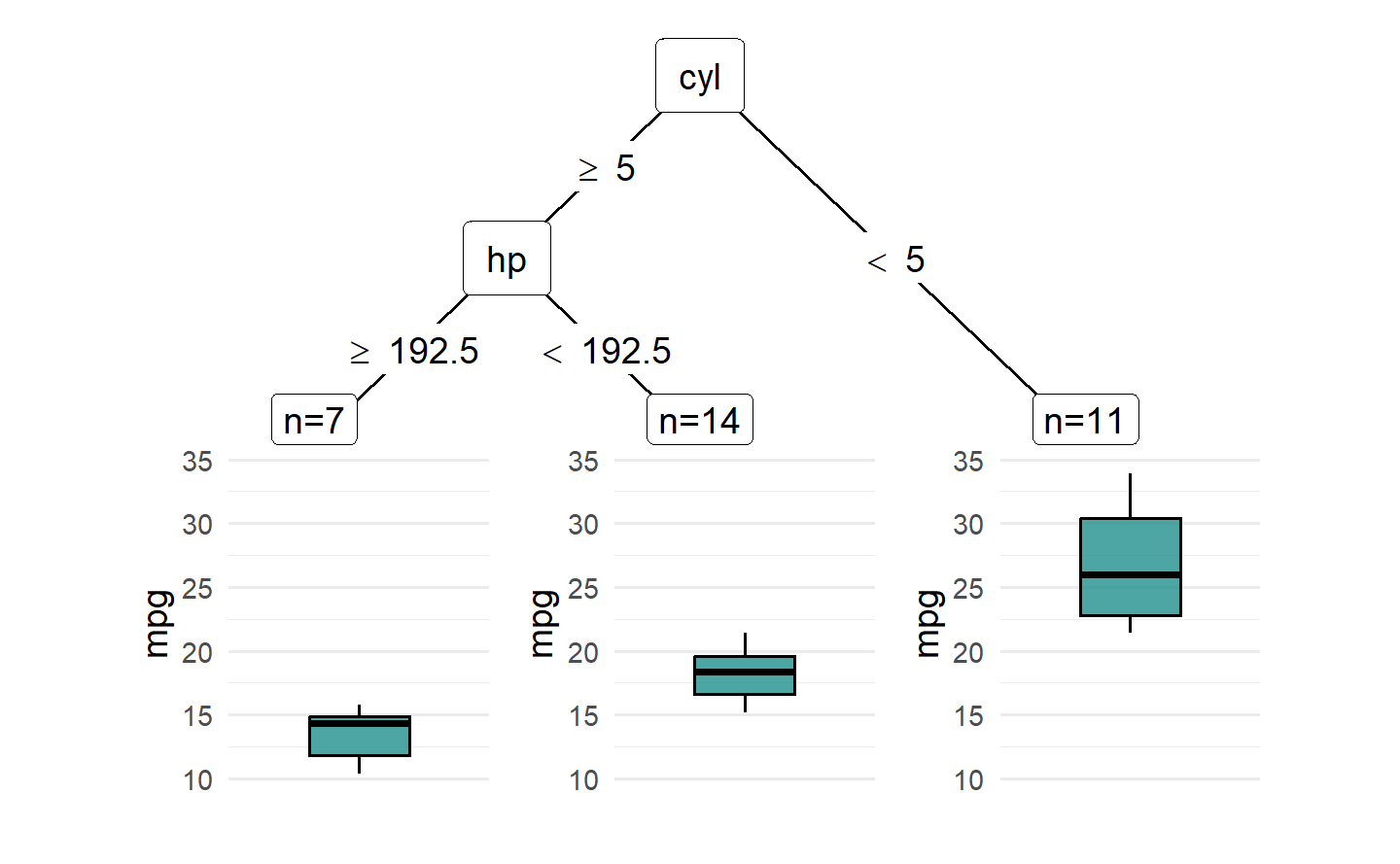
1.6.1.2 回归任务

task = tsk("mtcars")
task$select(c("am", "carb"))

autoplot(task, type = "target")  # "target" 图：箱线图展示目标变量的分布
autoplot(task, type = "pairs")   # "pairs" 图：展示多个特征与目标变量的成对比较

1.6.2 可视化学习器

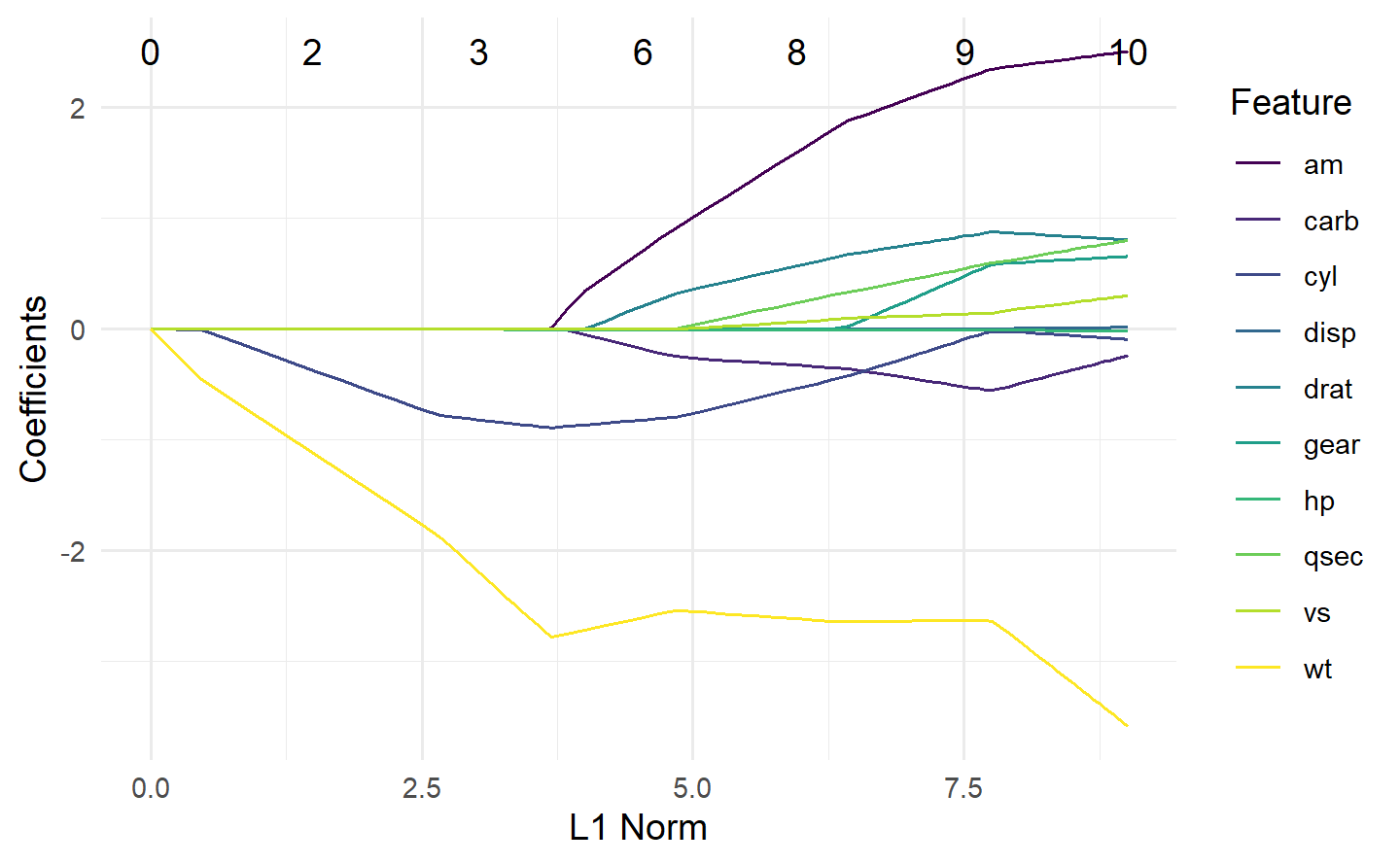
1.6.2.1 glmnet 回归学习器

task = tsk("mtcars")
learner = lrn("regr.glmnet")
learner$train(task)
autoplot(learner)

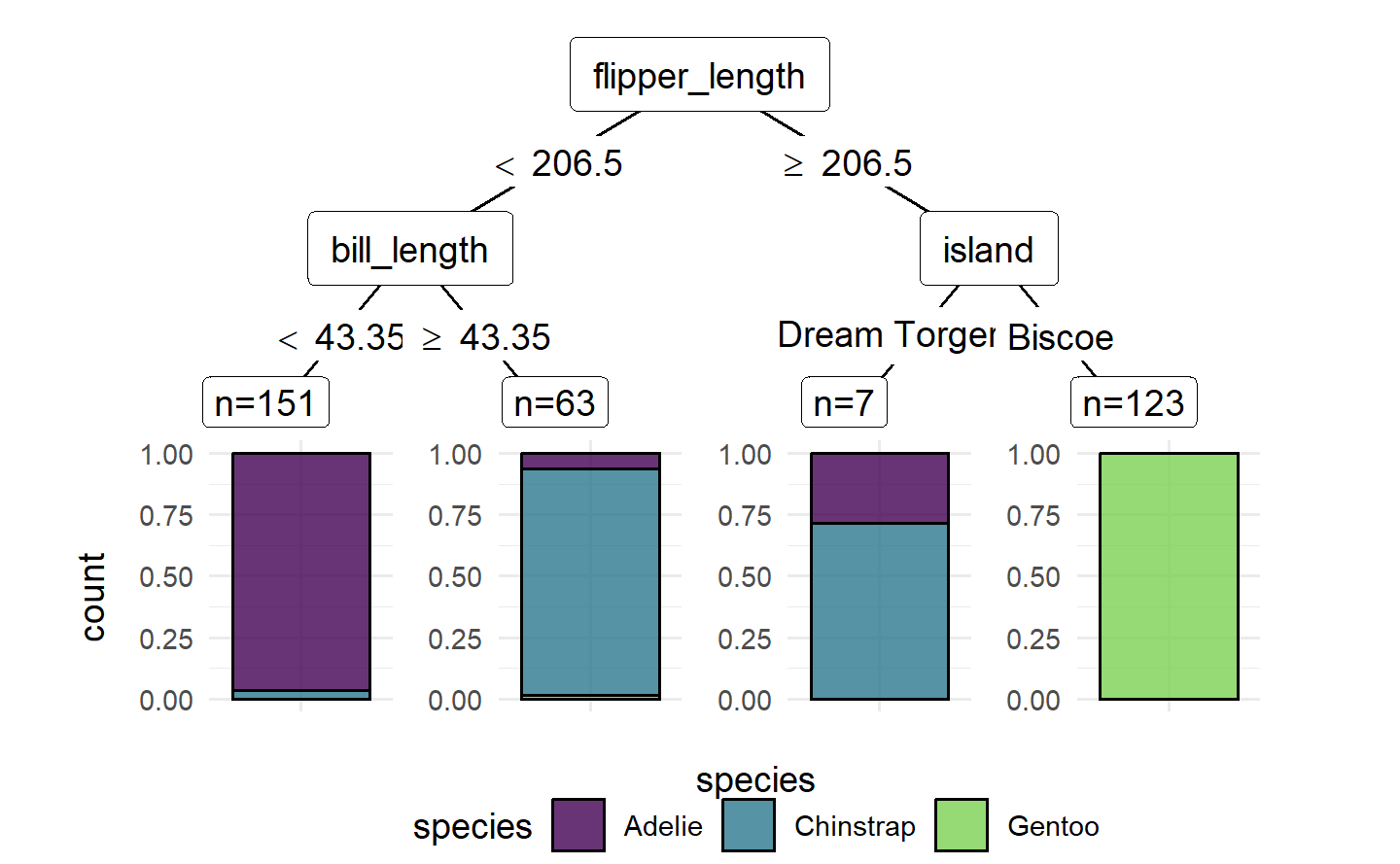
1.6.2.2 决策树学习器

# 分类树
task = tsk("penguins")
learner = lrn("classif.rpart", keep_model = TRUE)
learner$train(task)
autoplot(learner)

# 回归树
task = tsk("mtcars")
learner = lrn("regr.rpart", keep_model = TRUE)
learner$train(task)
autoplot(learner)

1.6.2.3 层次聚类学习器

# 层次聚类树
task = tsk("usarrests")
learner = lrn("clust.hclust")
learner$train(task)
autoplot(learner, type = "dend", task = task)

# 碎石图
autoplot(learner, type = "scree")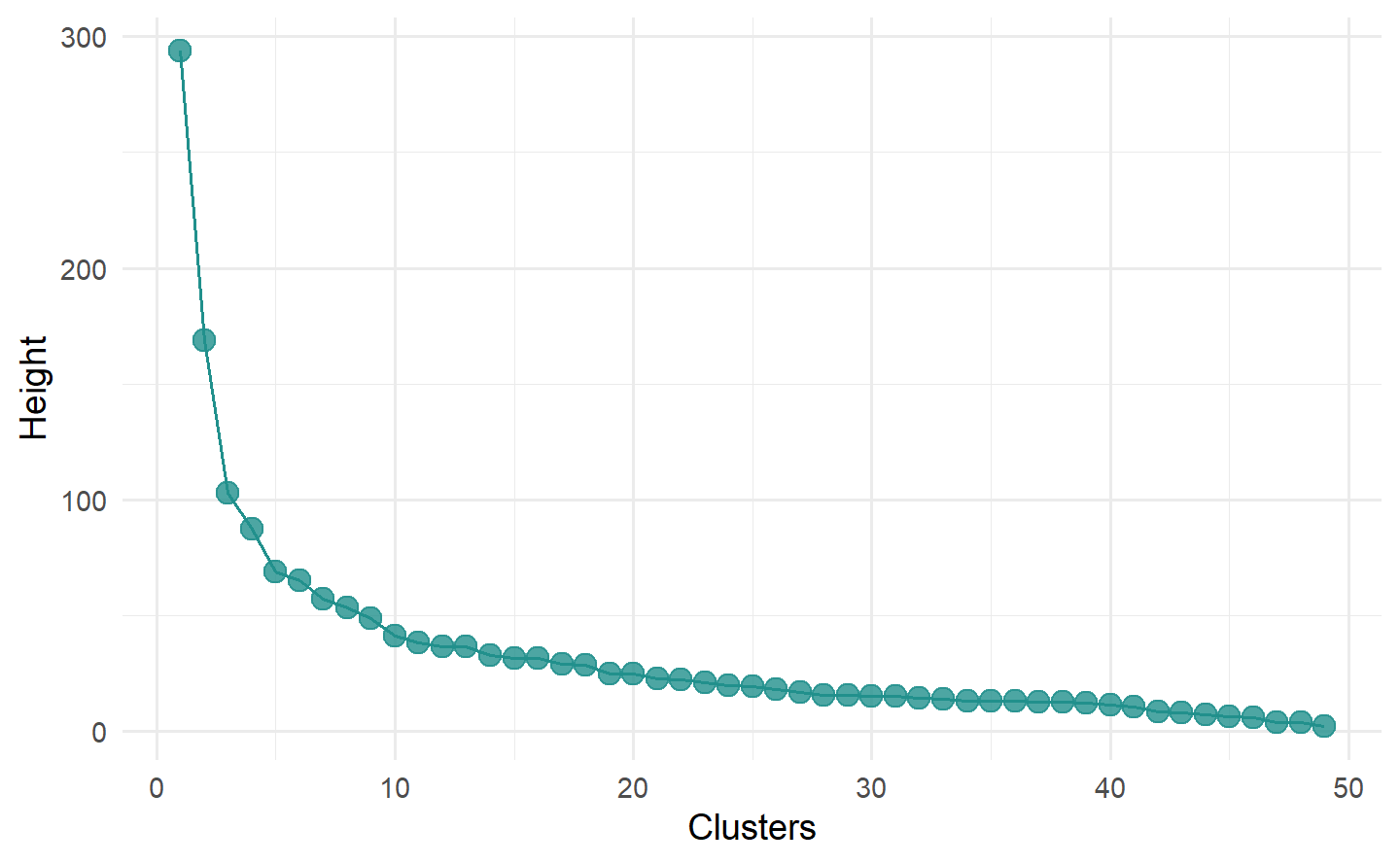

1.6.3 可视化预测对象

1.6.3.1 分类预测对象

# "stacked" 图：堆叠条形图展示预测类别和真实类别频数对比
task = tsk("spam")
learner = lrn("classif.rpart", predict_type = "prob")
pred = learner$train(task)$predict(task)
autoplot(pred, type = "stacked")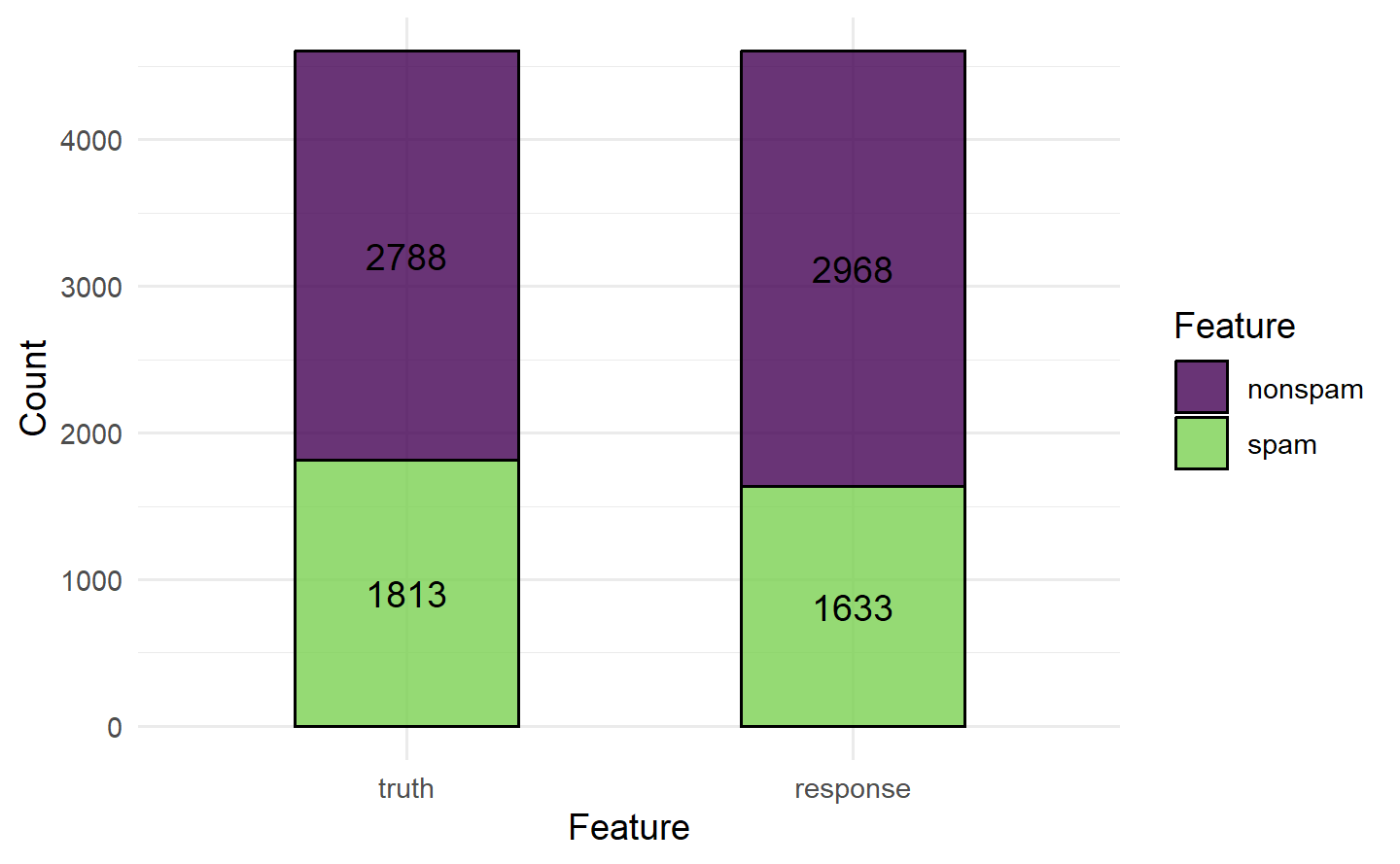

# ROC 曲线：展示不同阈值下的真阳率与假阳率
autoplot(pred, type = "roc")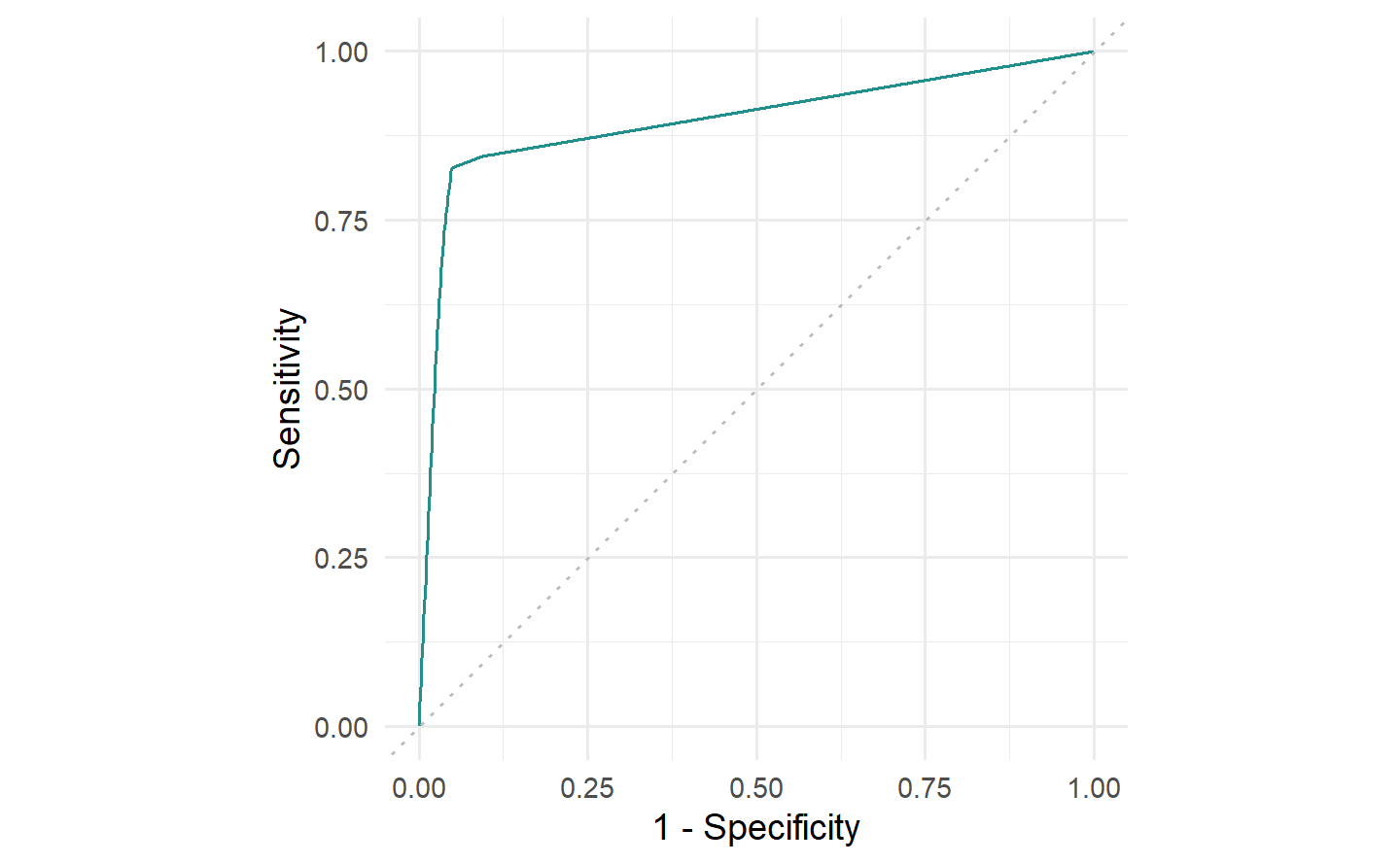

# PR 曲线：展示不同阈值下的查准率与召回率
autoplot(pred, type = "prc")

# “threshold” 图：展示二元分类在不同阈值下的性能
autoplot(pred, type = "threshold")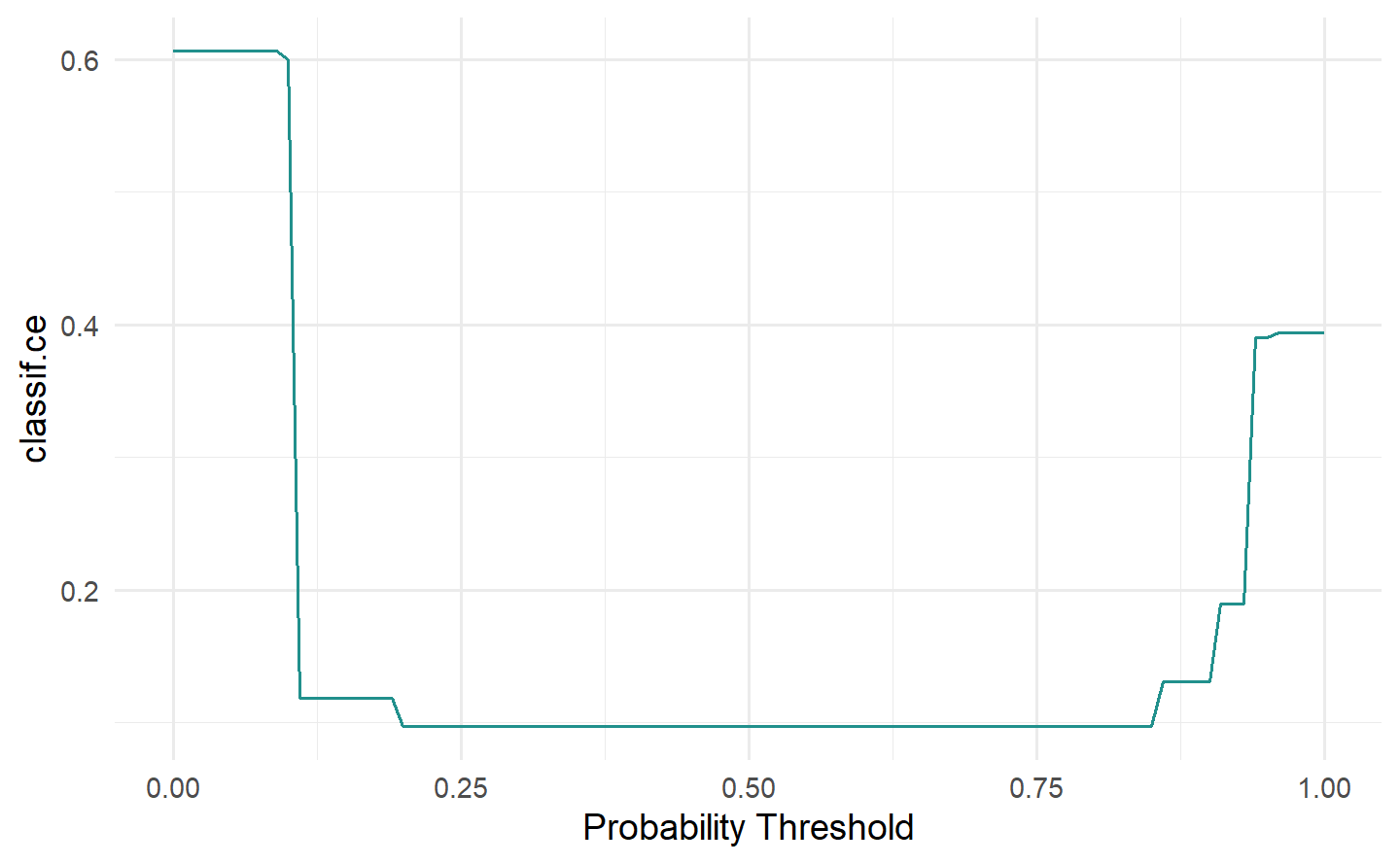

1.6.3.2 回归预测对象

# "xy" 图：散点图展示回归预测的真实值与预测值
task = tsk("boston_housing")
learner = lrn("regr.rpart")
pred = learner$train(task)$predict(task)
autoplot(pred, type = "xy")

# "residual" 图：绘制响应的残差图
autoplot(pred, type = "residual")

# "histogram" 图：残差直方图展示残差的分布
autoplot(pred, type = "histogram")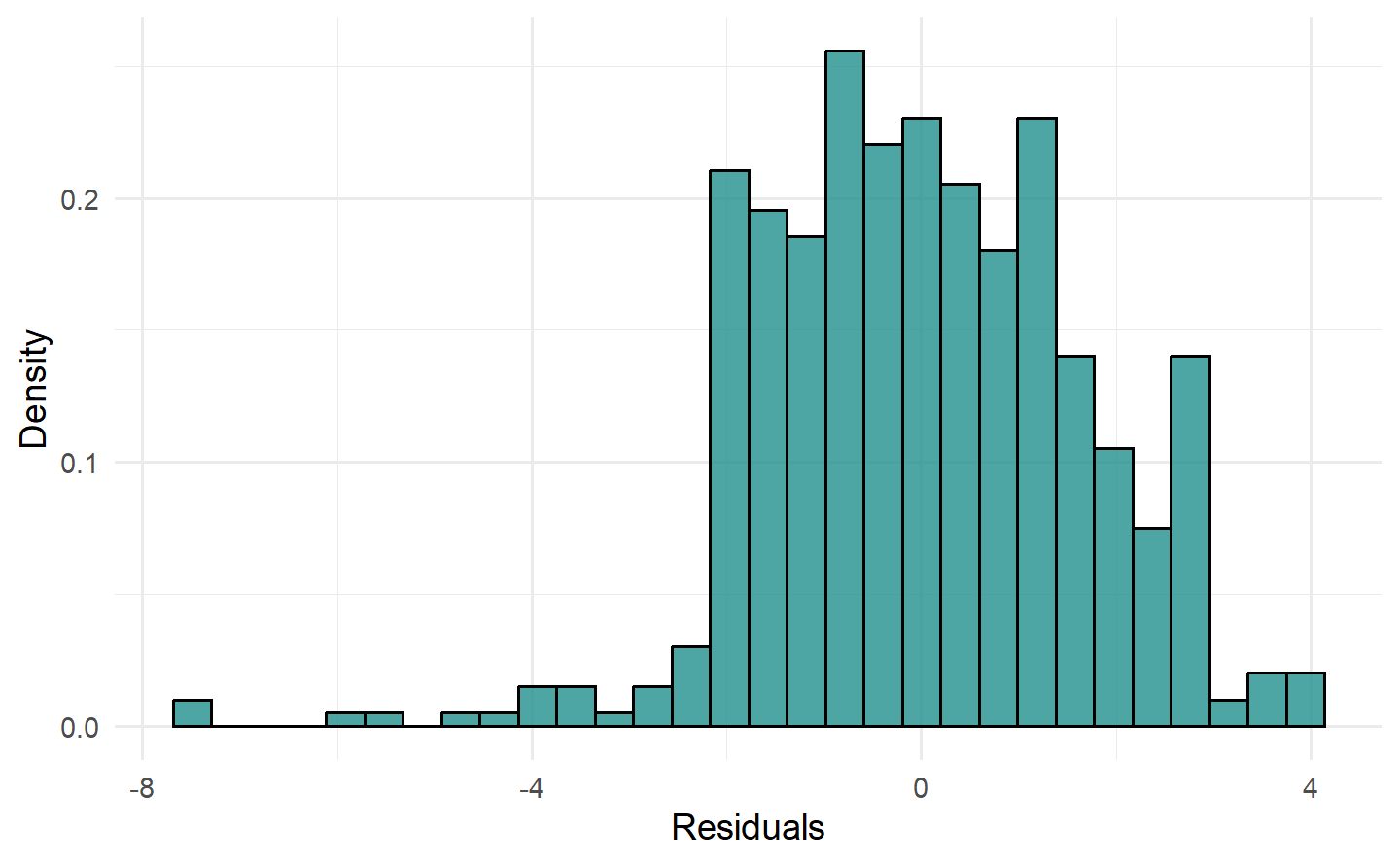

1.6.3.3 聚类预测对象

# "scatter" 图：绘制按聚类预测结果着色的散点图
task = tsk("usarrests")
learner = lrn("clust.kmeans", centers = 3)
pred = learner$train(task)$predict(task)
autoplot(pred, task, type = "scatter")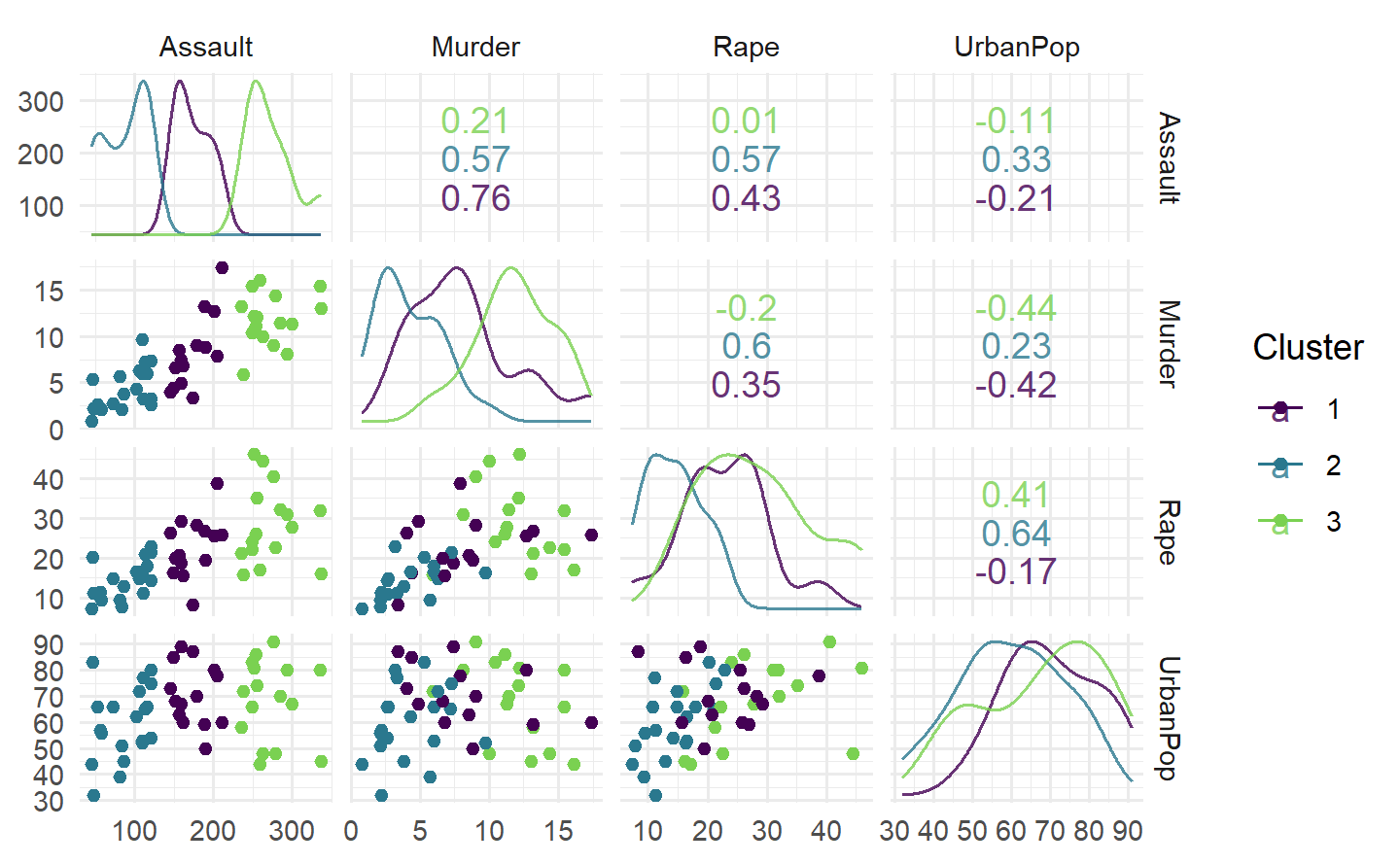

# "sil" 图：展示聚类的silhouette 宽度，虚线是平均silhouette 宽度
autoplot(pred, task, type = "sil")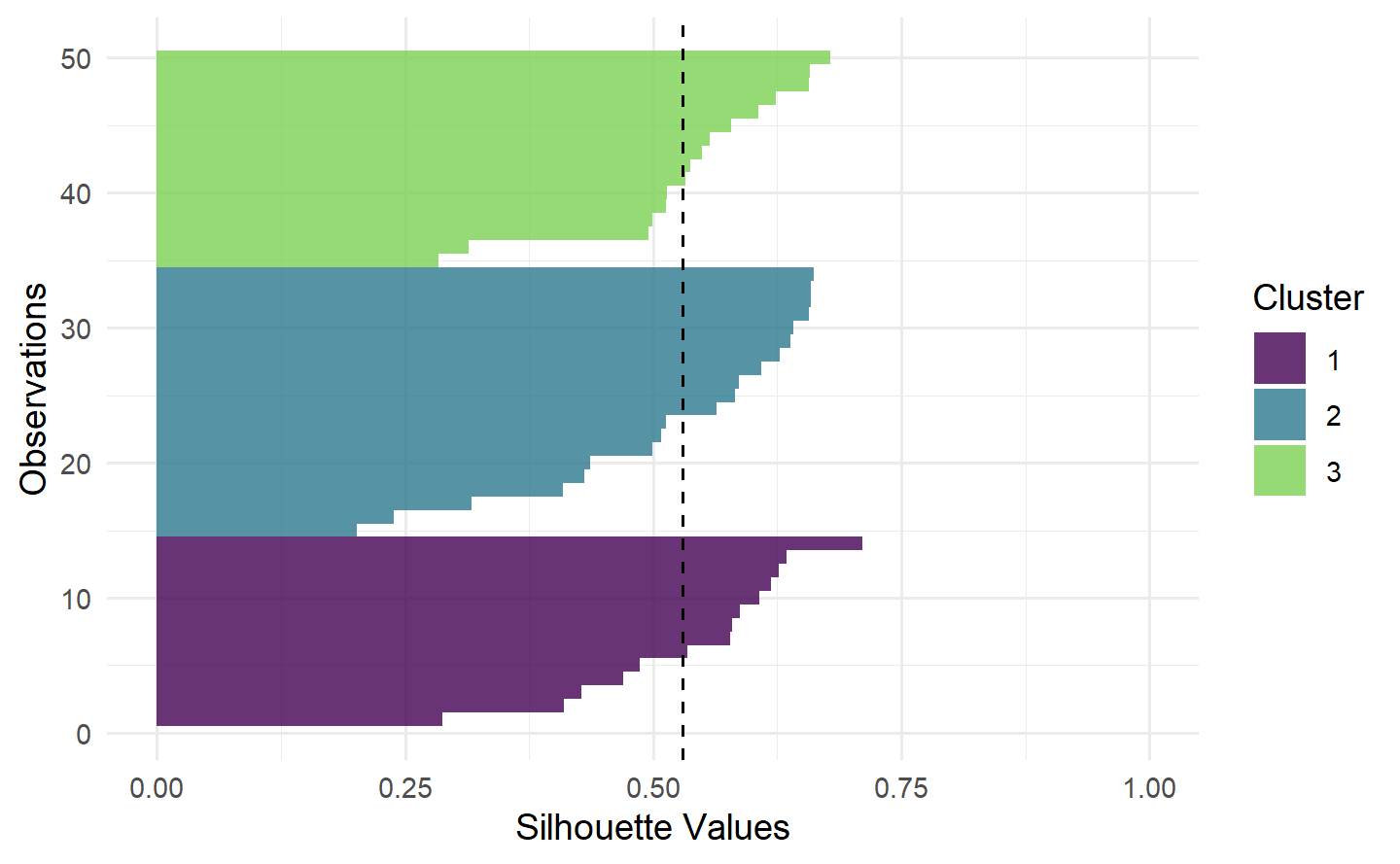

# "pca" 图：展示数据的前两个主成分，不同聚类用颜色区分
autoplot(pred, task, type = "pca")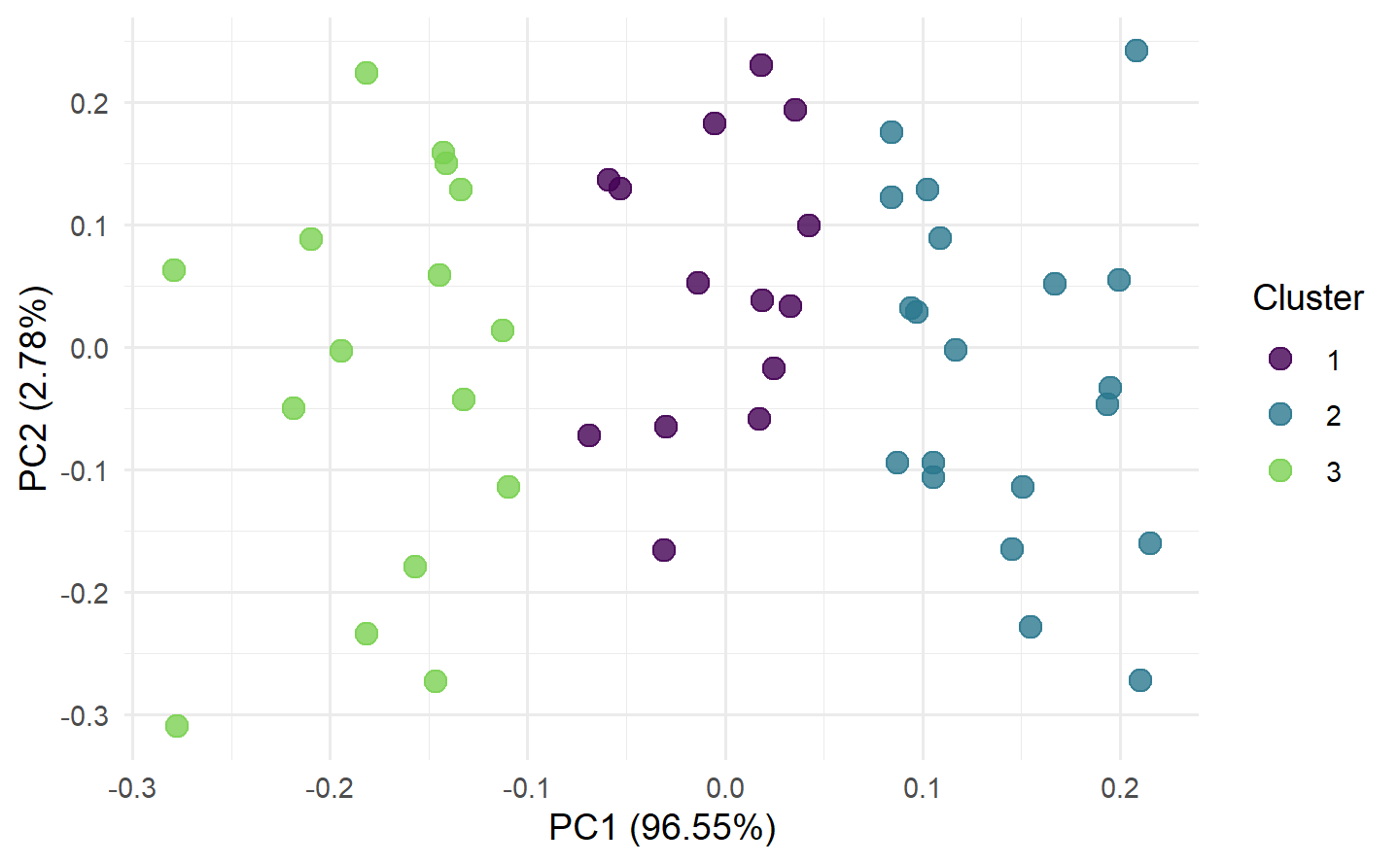

1.6.4 可视化重抽样结果

1.6.4.1 分类重抽样结果

# "boxplot"/"histogram" 图：箱线图展示性能度量的分布
task = tsk("sonar")
learner = lrn("classif.rpart", predict_type = "prob")
resampling = rsmp("cv")
rr = resample(task, learner, resampling)
autoplot(rr, type = "boxplot")
autoplot(rr, type = "histogram")
#> `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

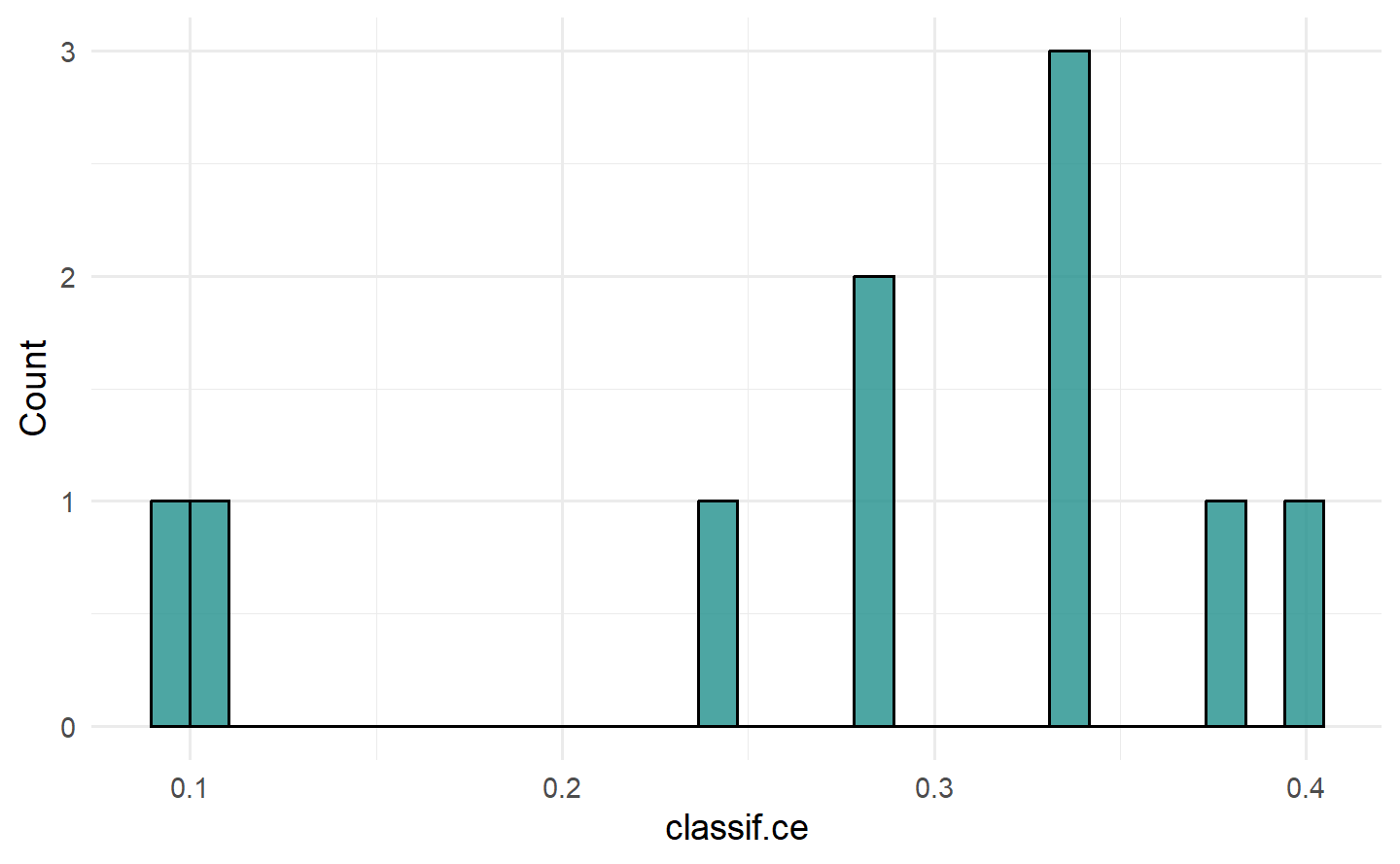
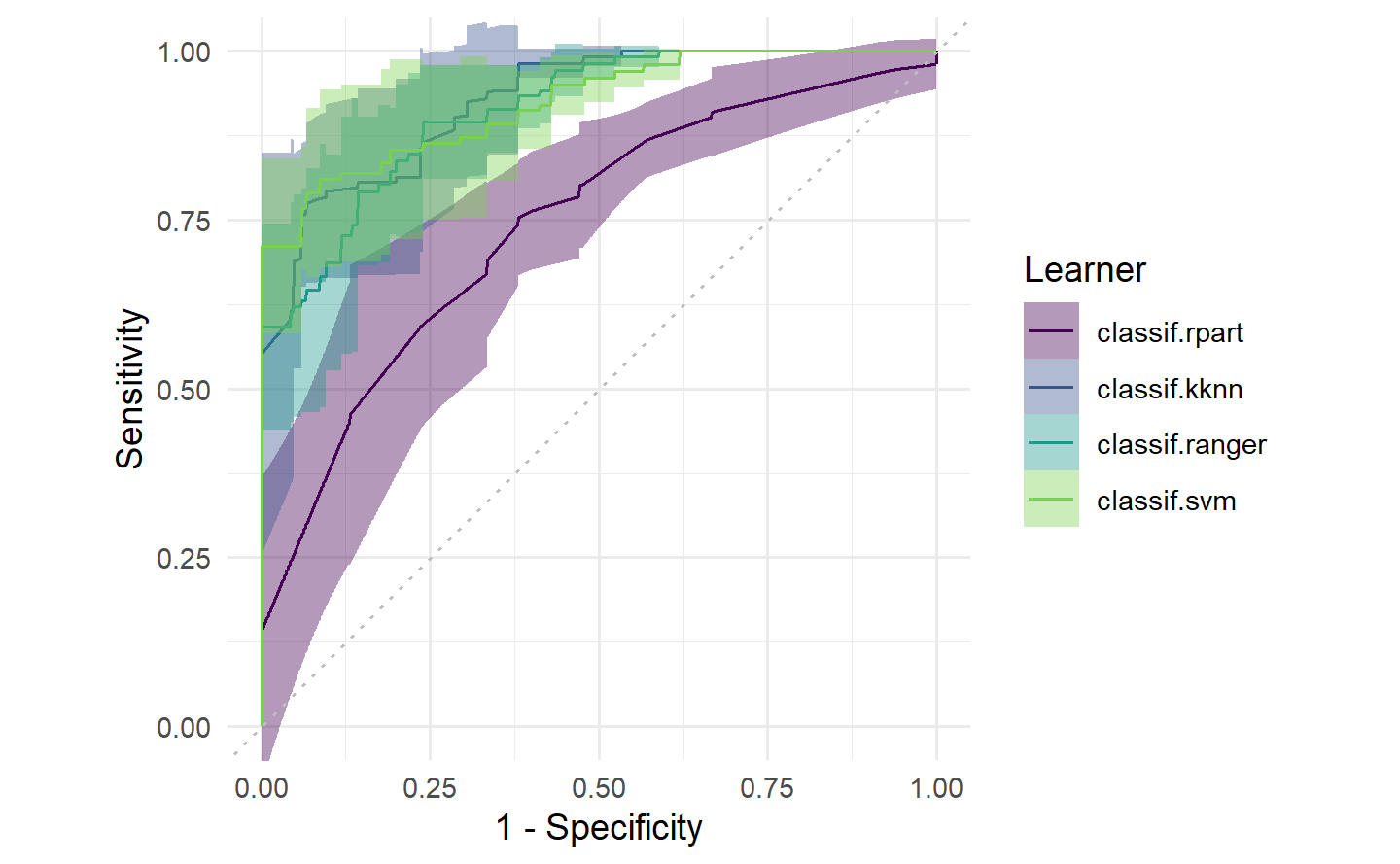
# ROC 曲线：展示不同阈值下的真阳率与假阳率
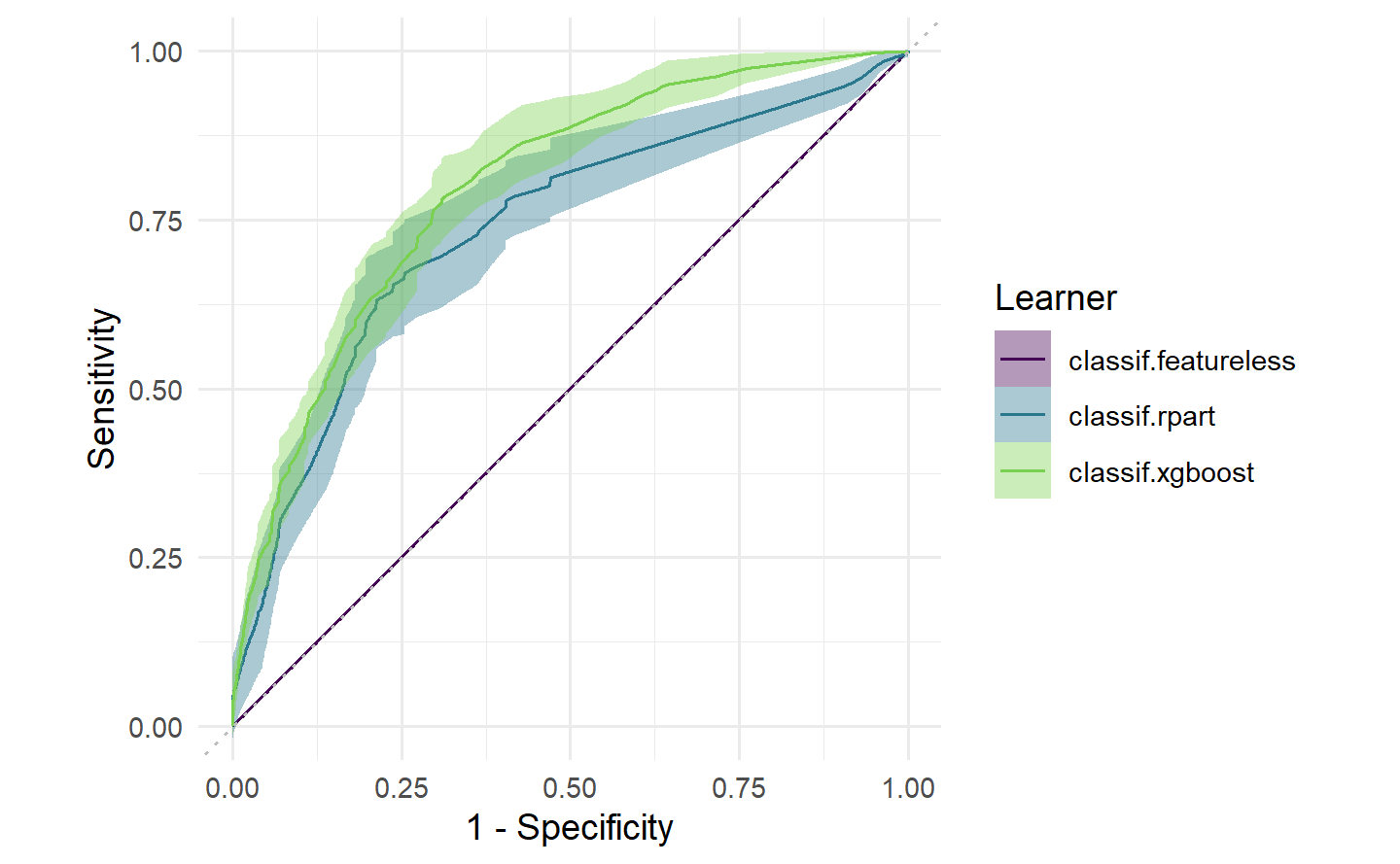
autoplot(rr, type = "roc")

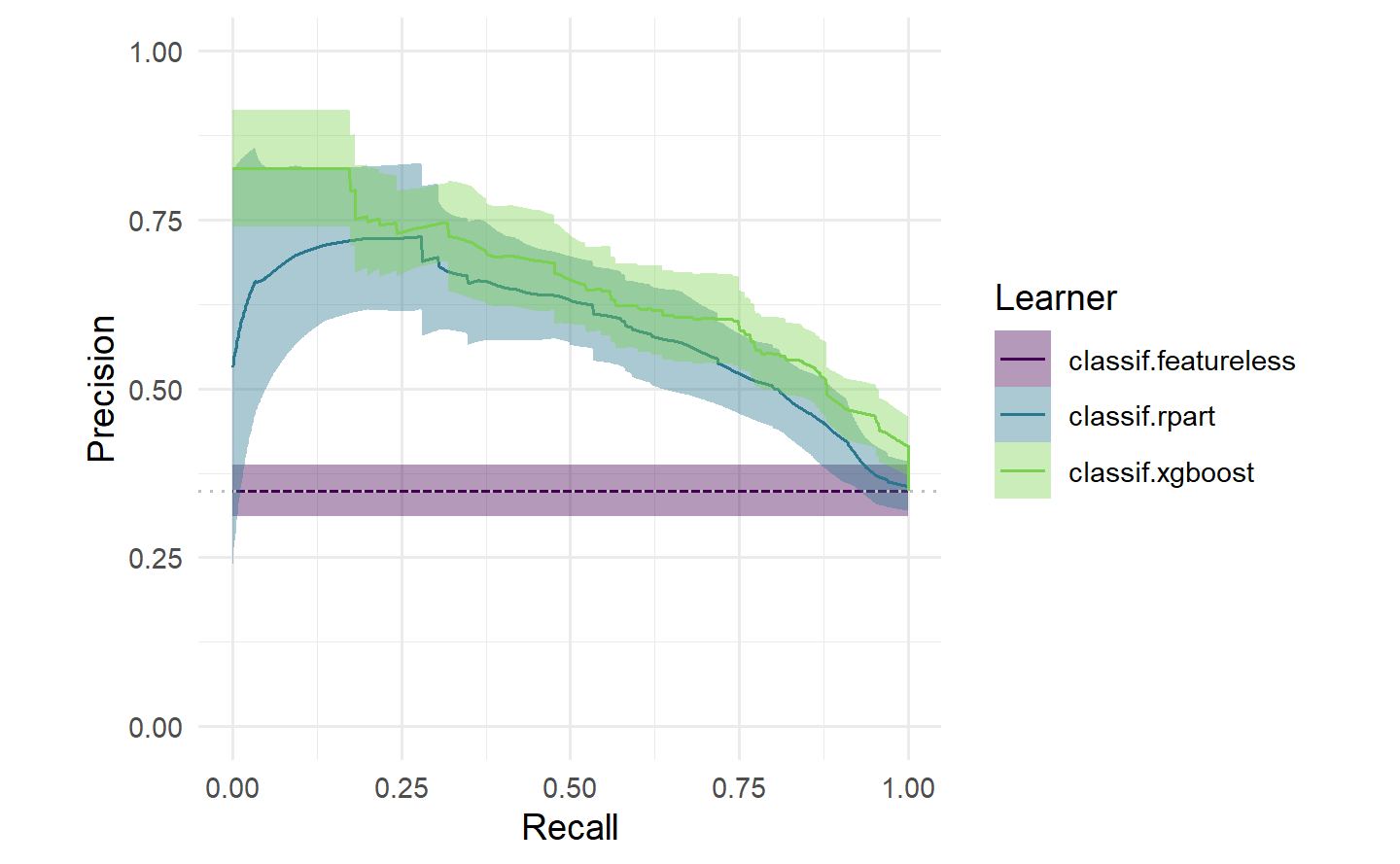
# PR 曲线：展示不同阈值下的查准率与召回率
autoplot(rr, type = "prc")

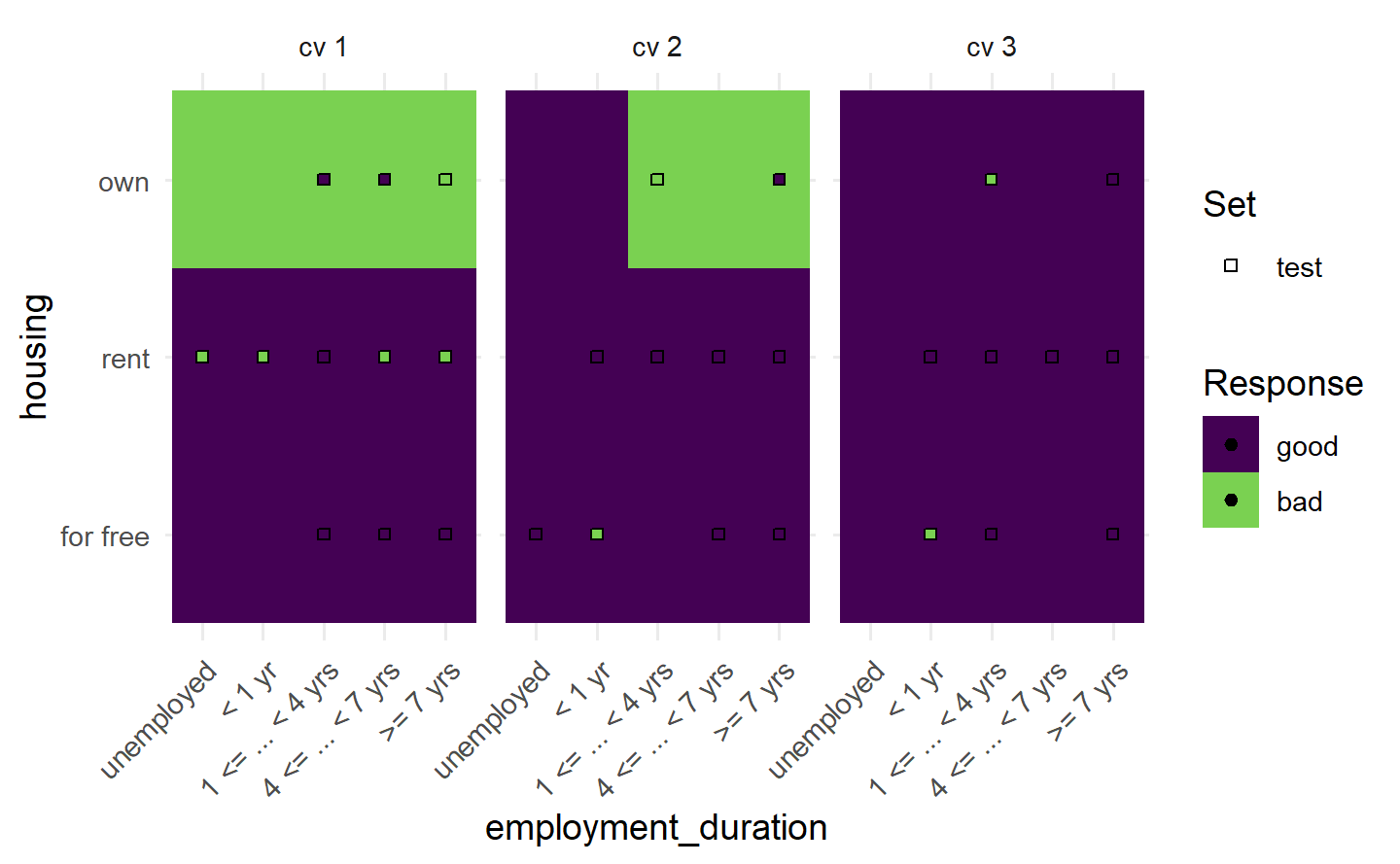
# "prediction" 图：展示两个特征表示的测试集样本点和以背景色区分的预测类别
task = tsk("pima")
task$filter(seq(100))
task$select(c("age", "glucose"))
learner = lrn("classif.rpart")
resampling = rsmp("cv", folds = 3)
rr = resample(task, learner, resampling, store_models = TRUE)
autoplot(rr, type = "prediction")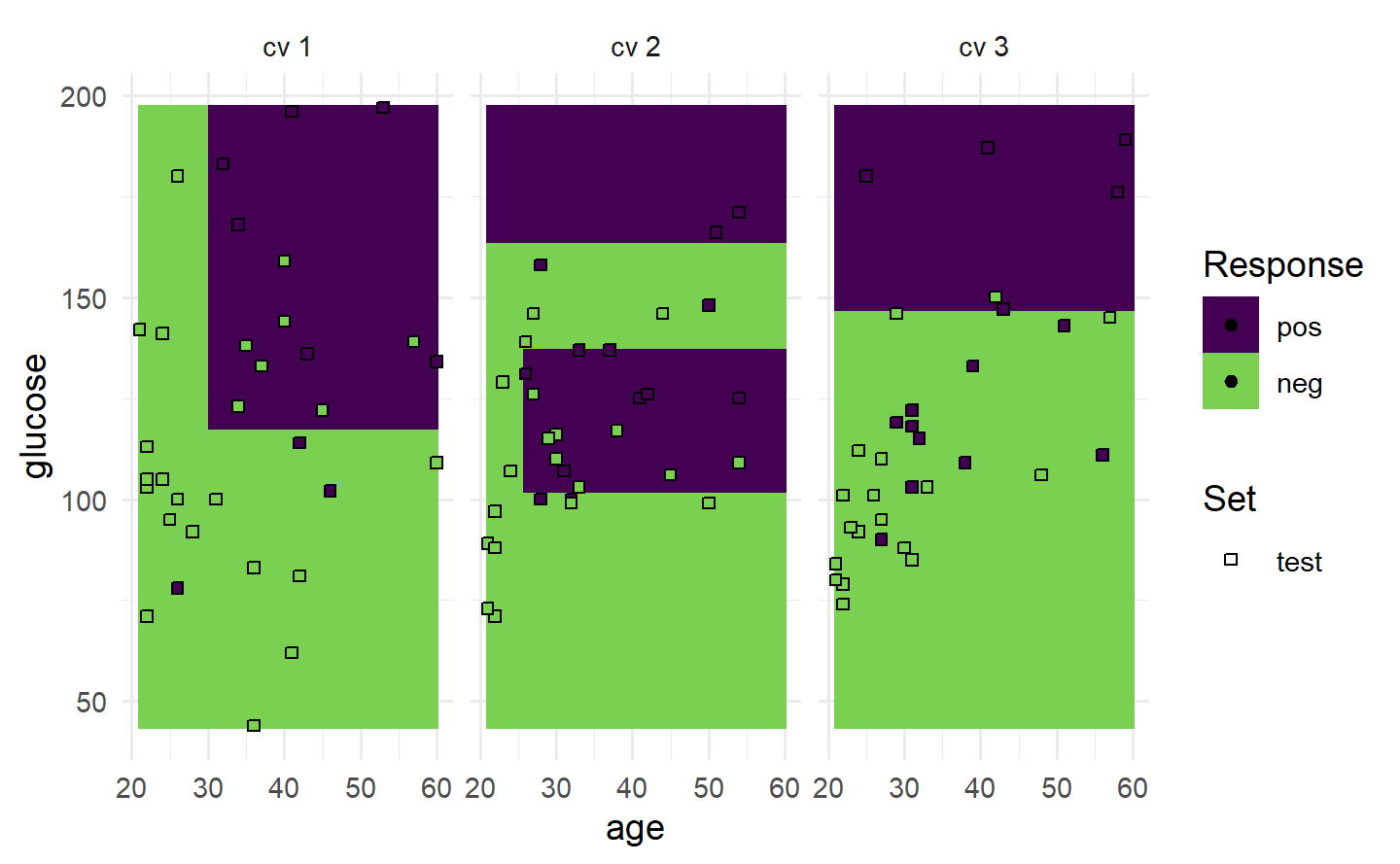

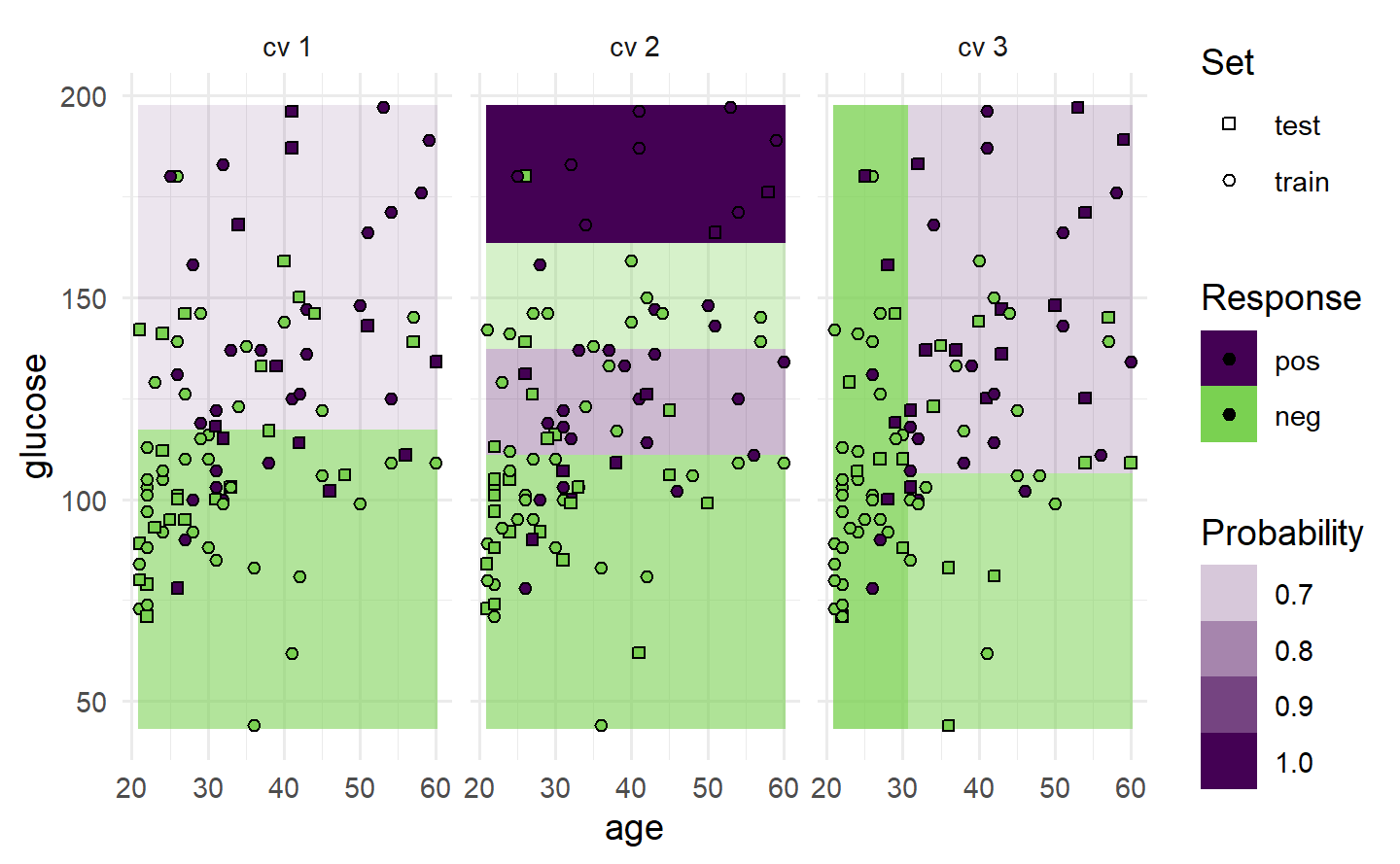
# 若将学习器的预测类型改为"prob"，则用颜色深浅展示概率值
learner = lrn("classif.rpart", predict_type = "prob")
resampling = rsmp("cv", folds = 3)
rr = resample(task, learner, resampling, store_models = TRUE)
autoplot(rr, type = "prediction")

# 上面是只绘制测试集，也可以加入训练集
learner = lrn("classif.rpart", predict_type = "prob",
              predict_sets = c("train", "test"))
resampling = rsmp("cv", folds = 3)
rr = resample(task, learner, resampling, store_models = TRUE)
autoplot(rr, type = "prediction",
         predict_sets = c("train", "test"))

# "prediction" 图也可以绘制分类特征
task = tsk("german_credit")
task$filter(seq(100))
task$select(c("housing", "employment_duration"))
learner = lrn("classif.rpart")
resampling = rsmp("cv", folds = 3)
rr = resample(task, learner, resampling, store_models = TRUE)
autoplot(rr, type = "prediction")

1.6.4.2 回归重抽样结果

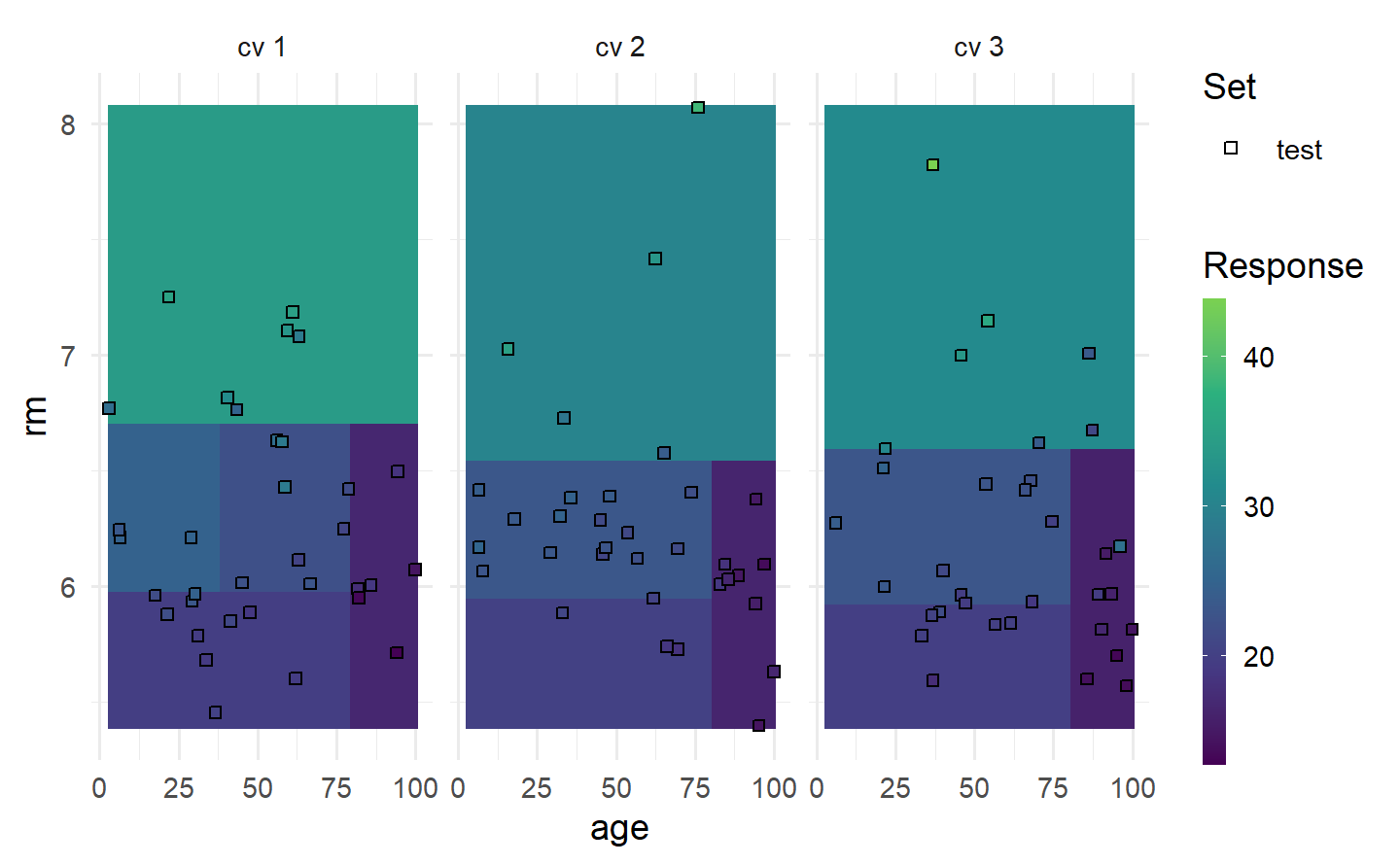
# "prediction" 图：绘制一个特征与响应的散点图，散点表示测试集中的观测
task = tsk("boston_housing")
task$select("age")
task$filter(seq(100))
learner = lrn("regr.rpart")
resampling = rsmp("cv", folds = 3)
rr = resample(task, learner, resampling, store_models = TRUE)
autoplot(rr, type = "prediction")

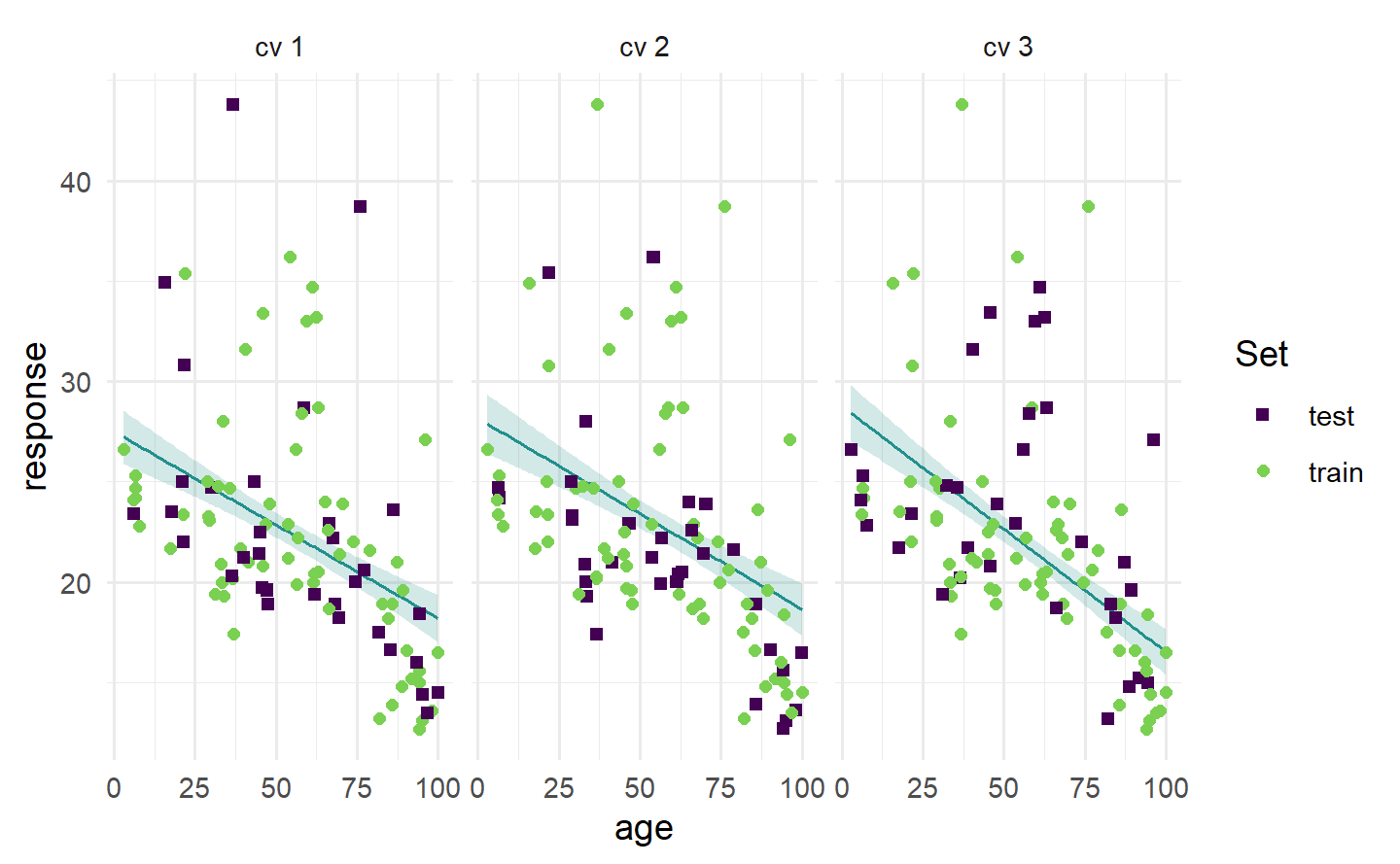
# 若将学习器的预测类型改为"se"，还可以加上置信带
learner = lrn("regr.lm", predict_type = "se")
resampling = rsmp("cv", folds = 3)
rr = resample(task, learner, resampling, store_models = TRUE)
autoplot(rr, type = "prediction")

# 上面是只绘制测试集，也可以加入训练集
task$select("age")
learner = lrn("regr.lm", predict_type = "se",
              predict_sets = c("train", "test"))
resampling = rsmp("cv", folds = 3)
rr = resample(task, learner, resampling, store_models = TRUE)
autoplot(rr, type = "prediction",
         predict_sets = c("train", "test"))

# 还可以将预测面添加到背景
task = tsk("boston_housing")
task$select(c("age", "rm"))
task$filter(seq(100))
learner = lrn("regr.rpart")
resampling = rsmp("cv", folds = 3)
rr = resample(task, learner, resampling, store_models = TRUE)
autoplot(rr, type = "prediction")

1.6.5 可视化基准测试结果

# "boxplot" 图：箱线图展示了多个任务的基准测试的性能分布
tasks = tsks(c("pima", "sonar"))
learners = lrns(c("classif.featureless", "classif.rpart", "classif.xgboost"),
                predict_type = "prob")
resampling = rsmps("cv")
bmr = benchmark(benchmark_grid(tasks, learners, resampling))
autoplot(bmr, type = "boxplot")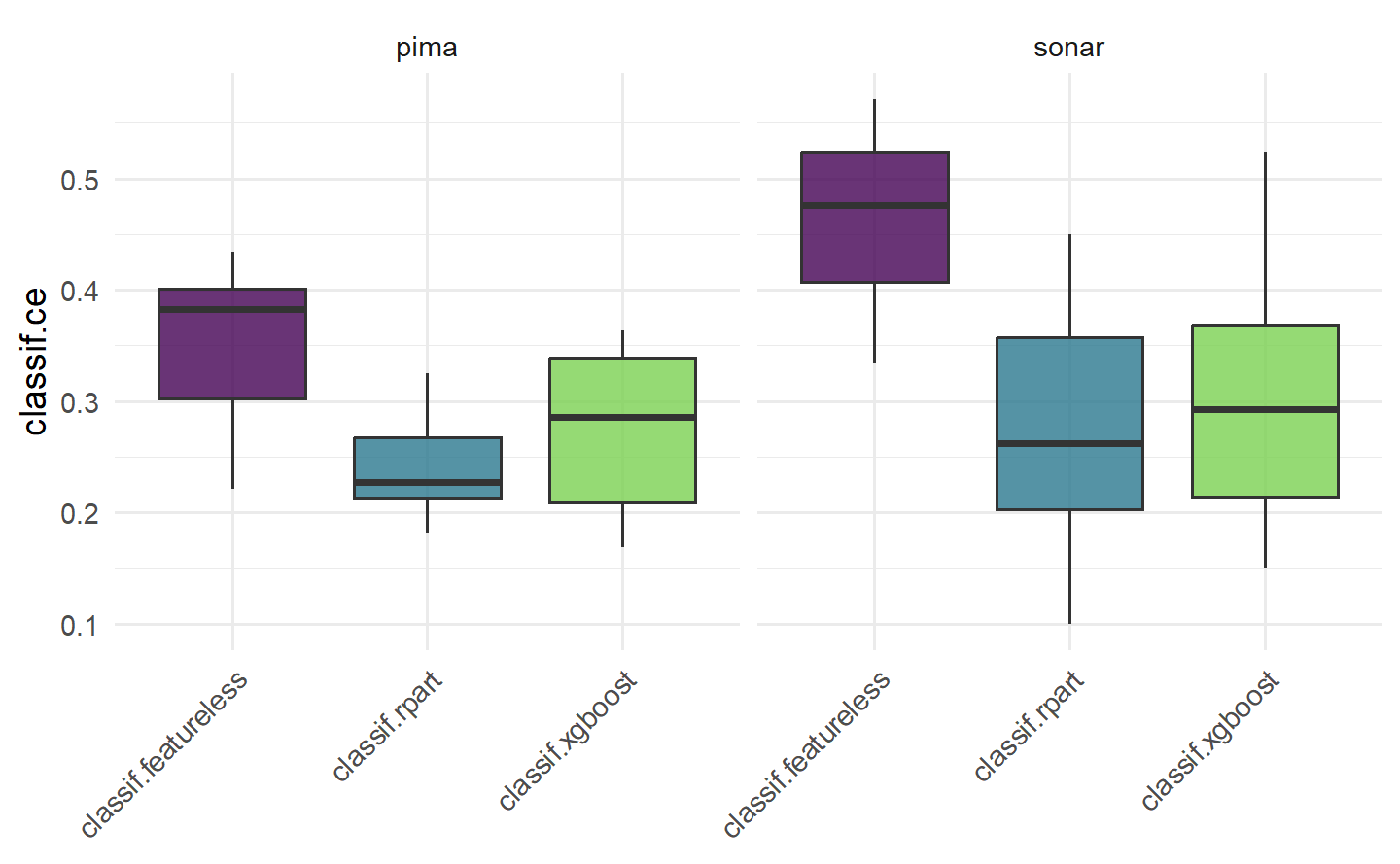

# 绘制一个任务与多个学习器的基准测试
task = tsk("pima")
learners = lrns(c("classif.featureless", "classif.rpart", "classif.xgboost"),
                predict_type = "prob")
resampling = rsmp("cv")
bmr = benchmark(benchmark_grid(task, learners, resampling))

autoplot(bmr, type = "roc")
autoplot(bmr, type = "prc")

1.6.6 可视化调参实例

# "performance" 图：散点折线图展示随批次的模型性能变化
instance = tune(
  tuner = tnr("gensa"),
  task = tsk("sonar"),
  learner = lts(lrn("classif.rpart")),
  resampling = rsmp("holdout"),
  measures = msr("classif.ce"),
  term_evals = 100
)
autoplot(instance, type = "performance")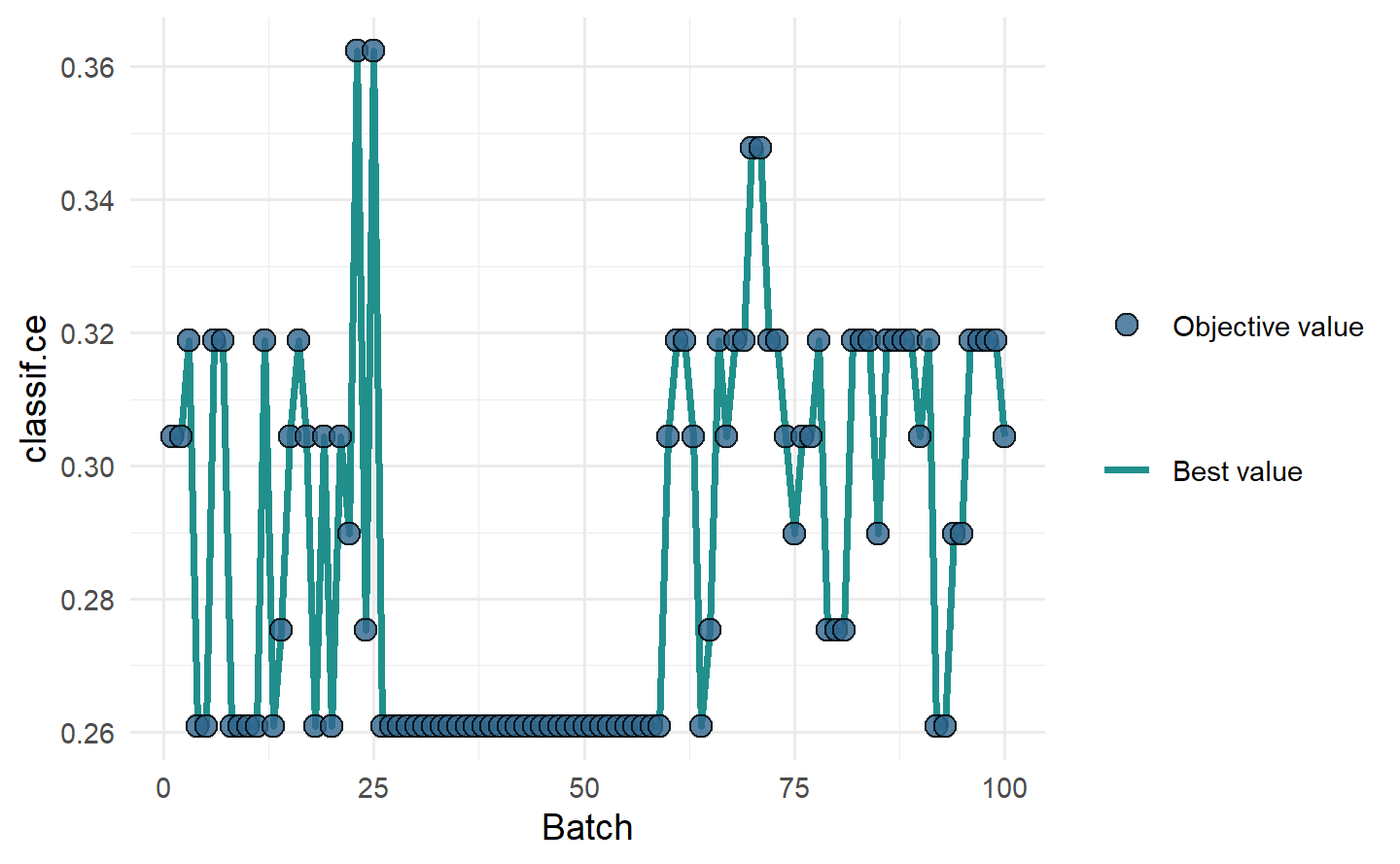

# "parameter" 图：散点图展示每个超参数取值与模型性能变化
autoplot(instance, type = "parameter", cols_x = c("cp", "minsplit"))

# "marginal" 图：展示不同超参数值的性能，颜色表示批次
autoplot(instance, type = "marginal", cols_x = "cp")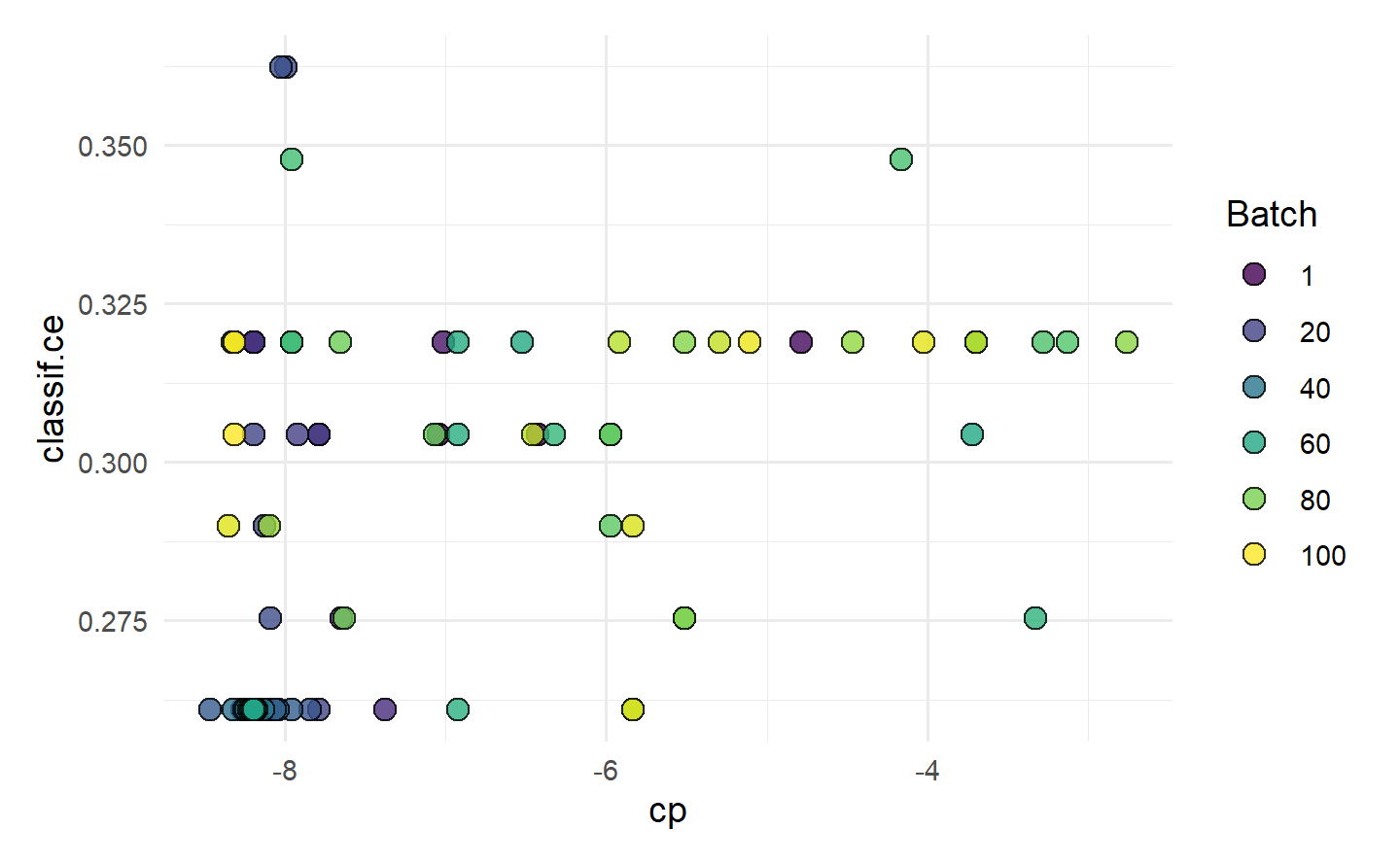

# "parallel" 图：可视化超参数之间的关系
autoplot(instance, type = "parallel")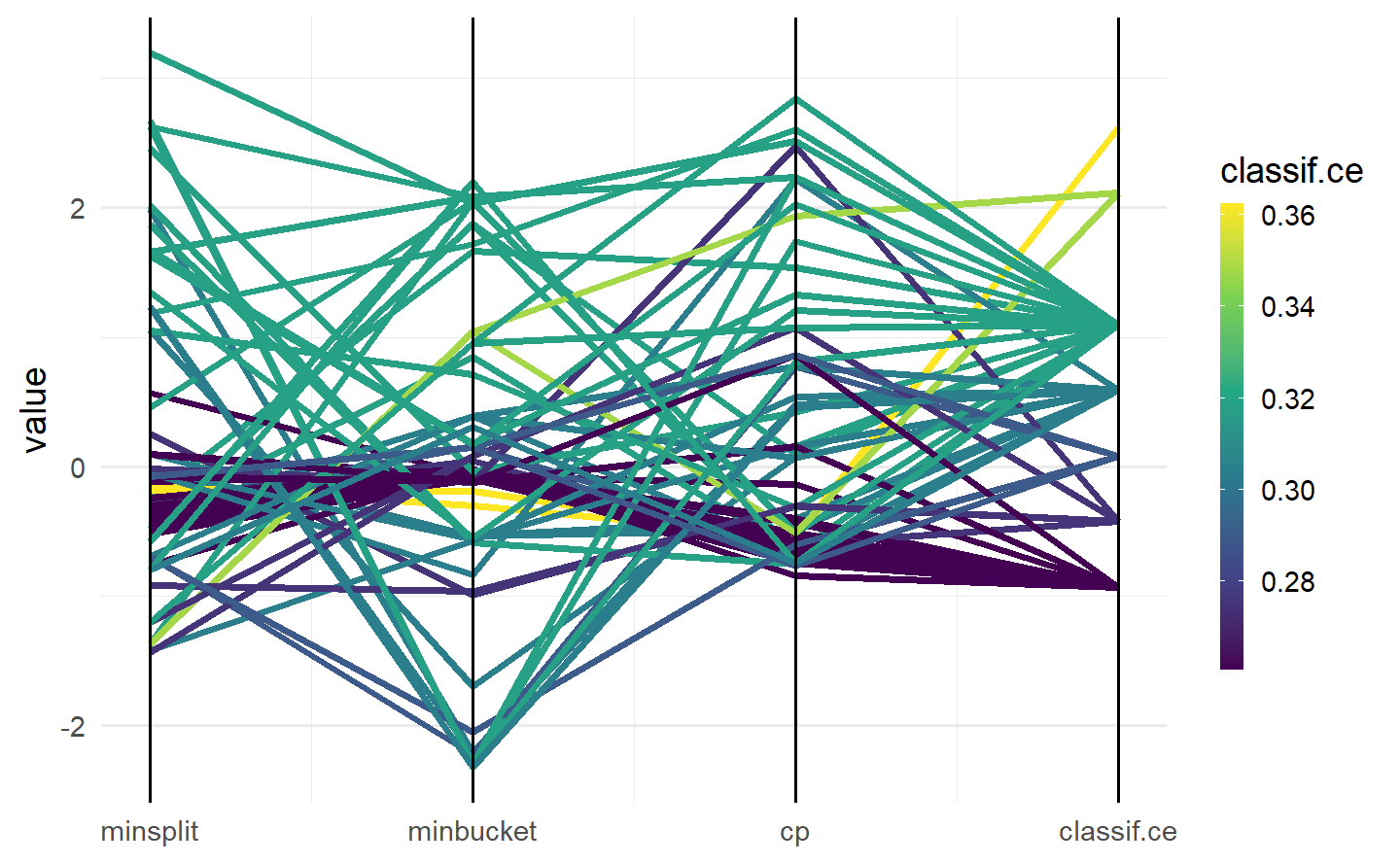

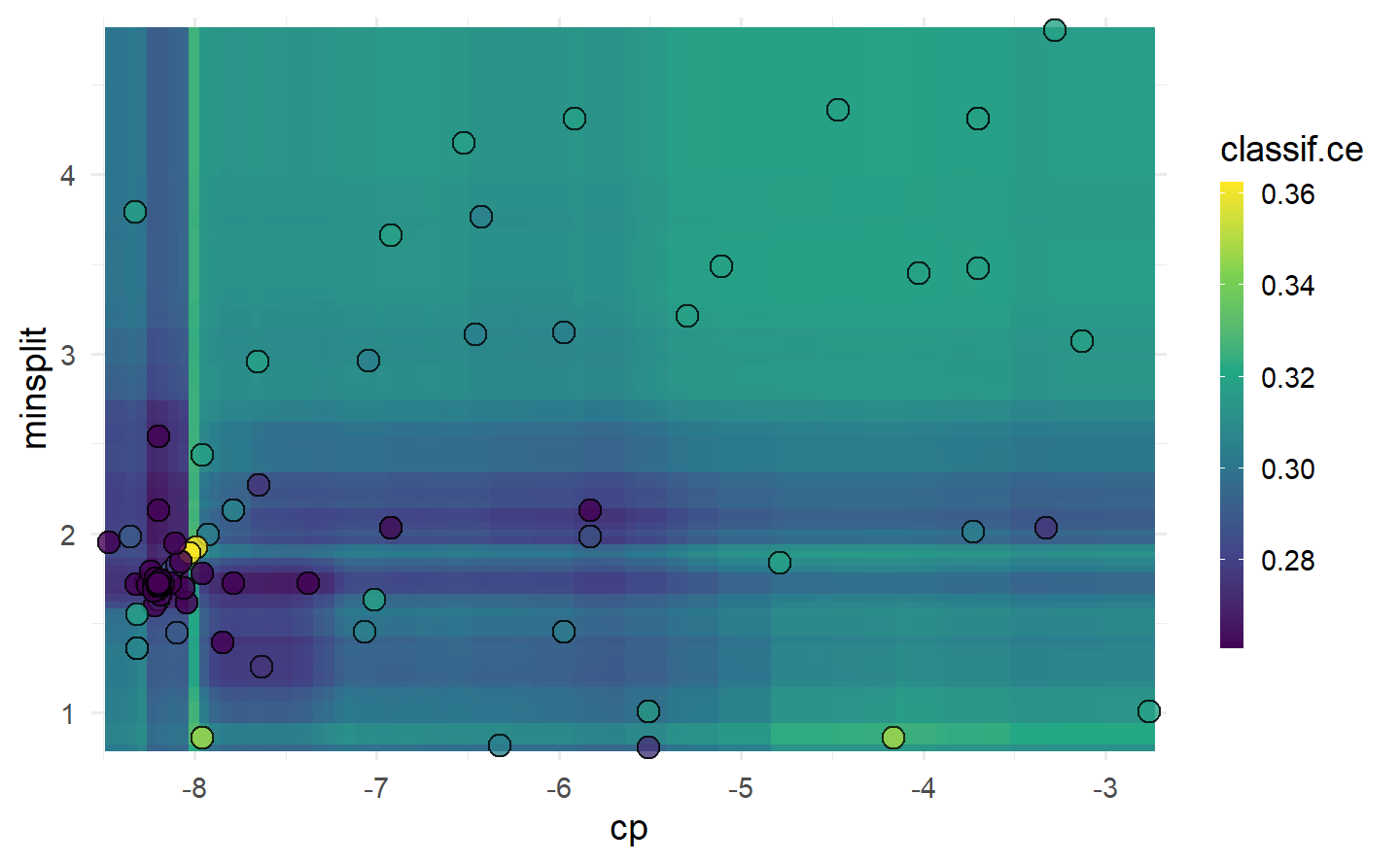
# "points" 图：散点热力图展示两个超参数的性能对比，用颜色深浅表示模型性能
autoplot(instance, type = "points", cols_x = c("cp", "minsplit"))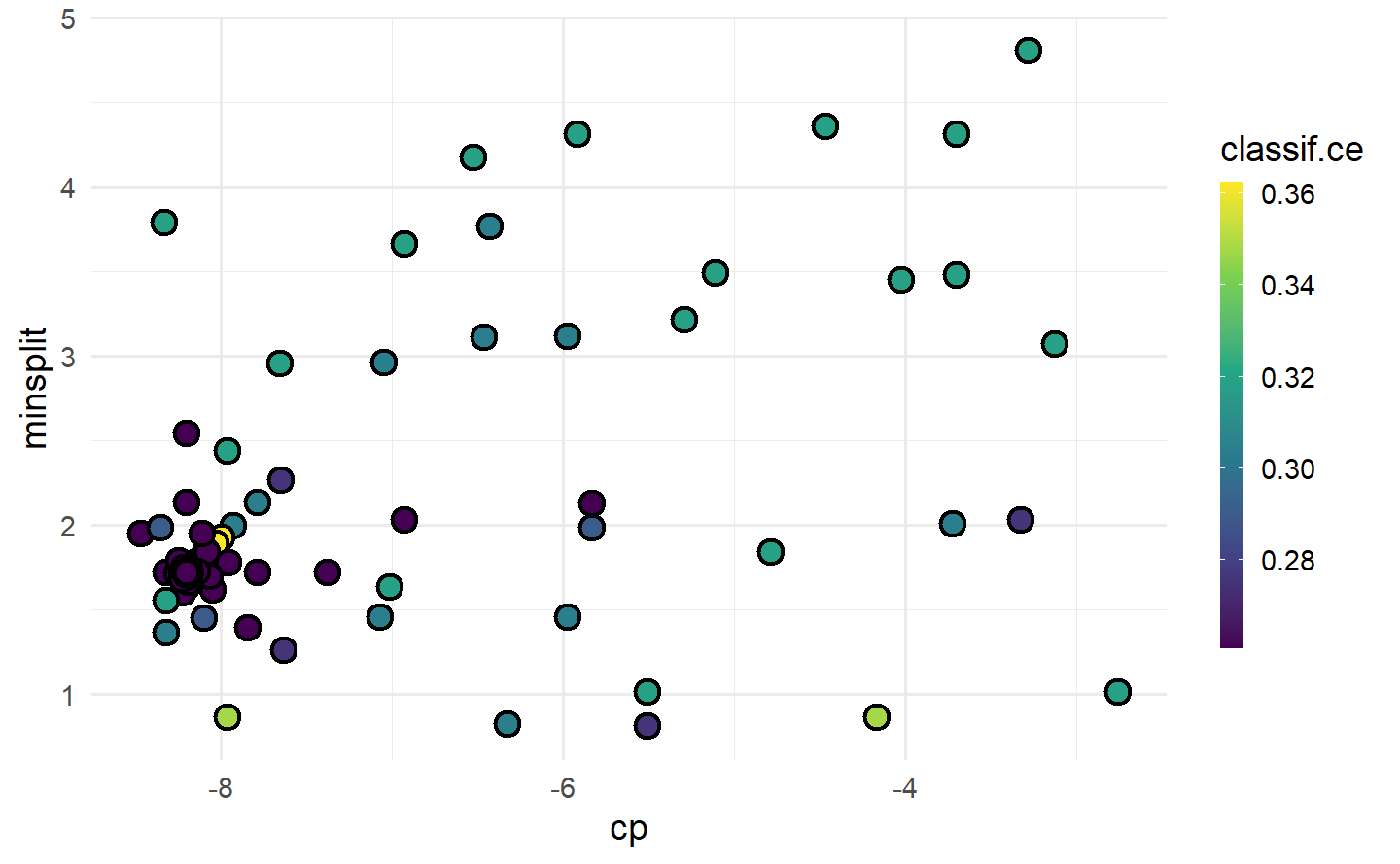

# "pairs" 图：展示所有超参数成对对比
autoplot(instance, type = "pairs")

# "surface" 图：绘制两个超参数的模型性能面，该面是用一个学习器插值的
autoplot(instance, type = "surface", cols_x = c("cp", "minsplit"),
         learner = lrn("regr.ranger"))

1.6.7 可视化特征过滤器

# 条形图展示基于过滤器的特征得分
task = tsk("mtcars")
ft = flt("correlation")
ft$calculate(task)
autoplot(ft, n = 5)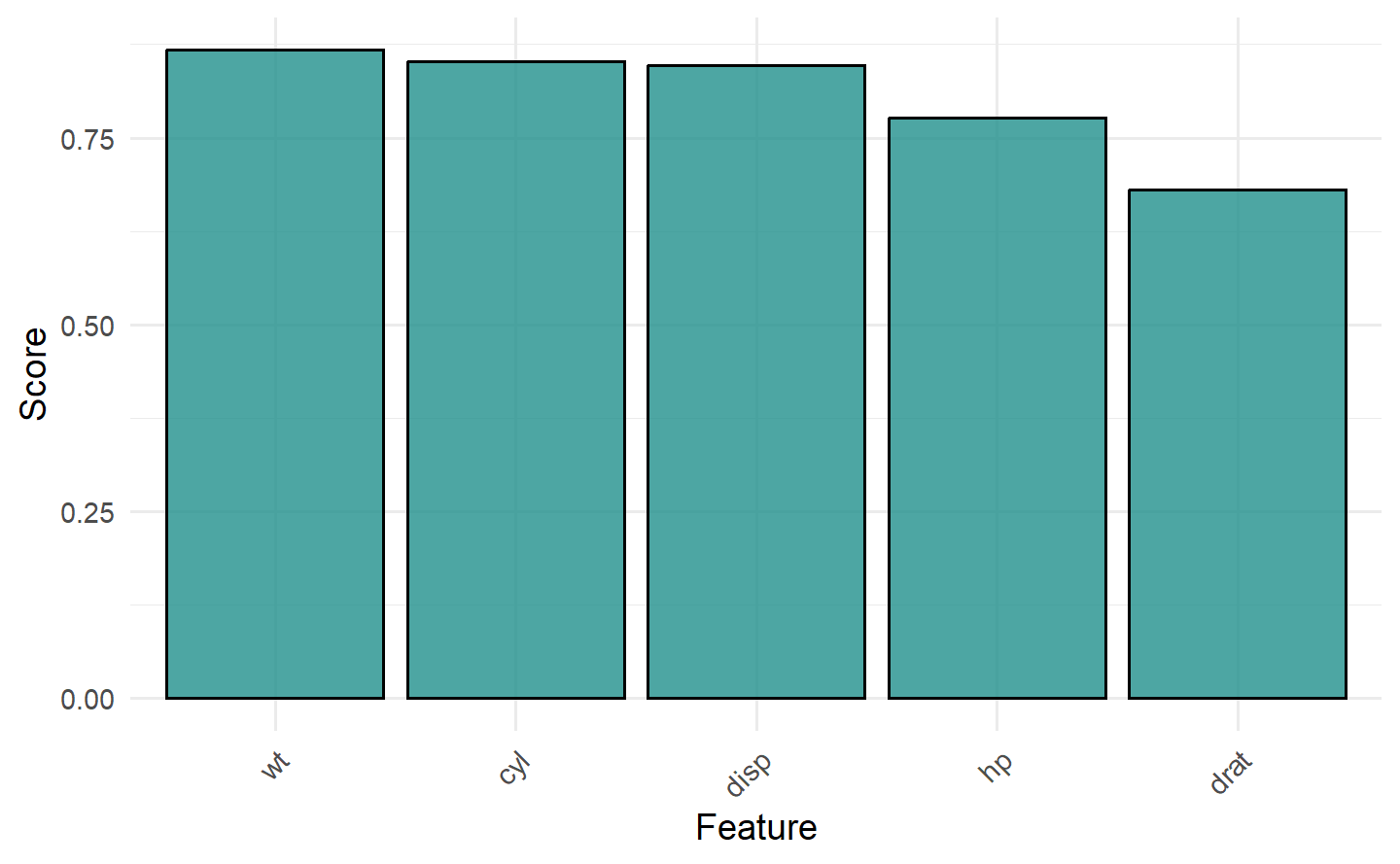

更多细节在 mlr3viz 包的 reference 页。

2 图学习器

一个管道运算（PipeOp），表示机器学习管道中的一个计算步骤。一系列的 PipeOps 通过边连接（%>>%）构成图（Graph），图可以是简单的线性图，也可以是复杂的非线性图。

搭建图学习器：

用 po() 获取 PipeOp，通过连接符 %>>% 连接 Graphs 与 PipeOps
通过 gunion() 将 Graphs 与 PipeOps 并起来
用 ppl("replicate", graph, n) 将 Graph 或 PipeOps 复制 n 份并起来
Graph$plot() 绘制图的结构关系
as_learner(Graph) 将图转化为学习器，即可跟普通学习器一样使用

管道、图学习器的主要用处在于：

特征工程：缺失值插补、特征提取、特征选择、处理不均衡数据……
集成学习：袋装法、堆叠法
分支训练、分块训练

2.1 线形图

# 搭建图
graph = po("scale") %>>%
  po("encode") %>>%
  po("imputemedian") %>>%
  lrn("classif.rpart")

# 可视化图
graph$plot()

# 转为图学习器
gl = as_learner(graph)

# 训练任务
task = tsk("iris")
gl$train(task)

调试图：

# 取出或设置图学习器超参数
graph$pipeops$scale$param_set$values$center = FALSE

# 获取单独PipeOp 的$state（经过$train() 后）
graph$keep_results = TRUE
graph$train(task)
#> $classif.rpart.output
#> NULL

graph$pipeops$scale$state$scale
#> Petal.Length  Petal.Width Sepal.Length  Sepal.Width 
#>     4.163367     1.424451     5.921098     3.098387

# 查看图的中间结果：$.result（需提前设置$keep_results = TRUE）
graph$pipeops$scale$.result[[1]]$head()
#>    Species Petal.Length Petal.Width Sepal.Length Sepal.Width
#> 1:  setosa    0.3362663    0.140405    0.8613268   1.1296201
#> 2:  setosa    0.3362663    0.140405    0.8275493   0.9682458
#> 3:  setosa    0.3122473    0.140405    0.7937718   1.0327956
#> 4:  setosa    0.3602853    0.140405    0.7768830   1.0005207
#> 5:  setosa    0.3362663    0.140405    0.8444380   1.1618950
#> 6:  setosa    0.4083234    0.280810    0.9119931   1.2587196

2.2 非线性图

2.2.1 分支

集成学习的袋装法、堆叠法都是非线性图，另一种非线性图是分支：即只执行若干条备选路径中的一条。

graph_branch = ppl("branch", list(
  pca = po("pca"),
  ica = po("ica")
)) %>>%
  lrn("classif.kknn")
graph_branch$plot()

2.2.2 分块训练

在数据太大，无法载入内存的情况下，一个常用的技术是将数据分成几块，然后分别对各块数据进行训练，之后再用 PipeOpClassifAvg 或 PipeOpRegrAvg 将模型按加权平均汇总。

graph_chunks = po("chunk", 4) %>>%
  ppl("greplicate", lrn("classif.rpart"), 4) %>>%
  po("classifavg", 4)
graph_chunks$plot()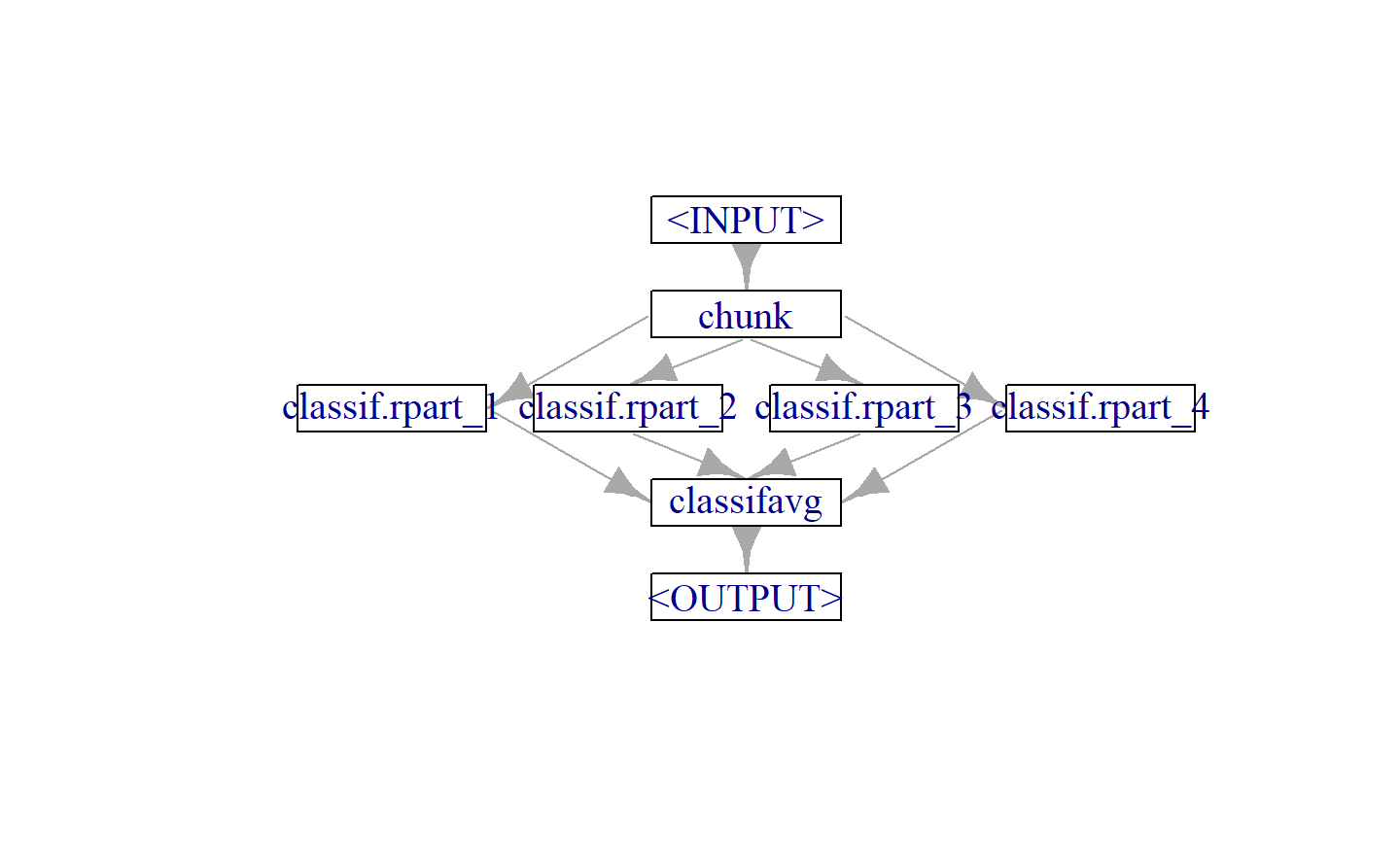

# 转化为图学习器，与学习器一样使用
chunks_lrn = as_learner(graph_chunks)
chunks_lrn$train(tsk("iris"))

2.3 集成学习

集成学习，是通过构建多个基学习器，并按一定策略结合成强学习器来完成学习任务，即所谓“博采众长”，最终效果是优于任何一个原学习器。集成学习可用于分类/回归集成、特征选择集成、异常值检测集成等。

这多个基学习器可以是同质的，比如都用决策树或都用神经网络，以 Bagging 和 Boosting 模式为代表；也可以是异质的，即采用不同的算法，以 Stacking 模式为代表。

2.3.1 装袋法（Bagging）

Bagging 采用的是并行机制，即基学习器的训练之间没有前后顺序可以同时进行。

Bagging 是用“有放回” 抽样（Bootstrap 法）的方式抽取训练集，对于包含 $m$ 个样本的训练集，进行 $m$ 次有放回的随机抽样操作，得到样本子集（有重复）中有接近 36.8% 的样本没有被抽到。

按照同样的方式重复进行，就可以采集到 $T$ 个包含 $m$ 个样本的数据副本，从而训练出 $T$ 个基学习器。

最终对这 $T$ 个基学习器的输出进行结合，分类问题就采用“多数决”，回归问题就采用“取平均”。

# 单分支：数据子抽样 + 决策树
single_path = po("subsample") %>>% lrn("classif.rpart")
# 复制 10 次得到 10 个分支，再接类平均
graph_bag = ppl("greplicate", single_path, n = 10) %>>%
  po("classifavg")
# 可视化结构关系
graph_bag$plot()

# 转为图学习器，可与普通学习器一样使用
baglrn = as_learner(graph_bag)
baglrn$train(tsk("iris"))

2.3.2 提升法（Boosting）

Boosting 采用的是串行机制，即基学习器的训练存在依赖关系，按次序一一进行训练（实现上可以做到并行）。

基本思想：基模型的训练集按照某种策略每次都进行一定的转化，对所有基模型预测的结果进行线性合成产生最终的预测结果。

从偏差-方差分解来看，Boosting 算法主要关注于降低偏差，每轮的迭代都关注于训练过程中预测错误的样本，将弱学习器提升为强学习器。

2.3.3 堆叠法（Stacking）

Stacking 法，采用的是分阶段机制，将若干基模型的输出作为输入，再接一层主学习器，得到最终的预测。

将训练好的所有基模型对训练集进行预测，第 $j$ 个基模型对第 $i$ 个训练样本的预测值将作为新的训练集中第 $i$ 个样本的第 $j$ 个特征值，最后基于新的训练集进行训练。同理，预测的过程也要先经过所有基模型的预测形成新的测试集，最后再对测试集进行预测。

用于堆叠的基模型通常采用不同的模型，作用在相同的训练集上。

为了充分利用数据，Stacking 通常采用 $k$ 折交叉训练法（类似 $k$ 折交叉验证）：每个基学习器分别在各个 $k-1$ 折数据上训练，在其剩下的 1 折数据上预测，就可以得到对任意 1 折数据的预测结果，进而用于训练主模型。

graph_stack = gunion(list(
  po("learner_cv", lrn("regr.lm")),
  po("learner_cv", lrn("regr.svm")),
  po("nop")
)) %>>%
  po("featureunion") %>>%
  lrn("regr.ranger")

graph_stack$plot()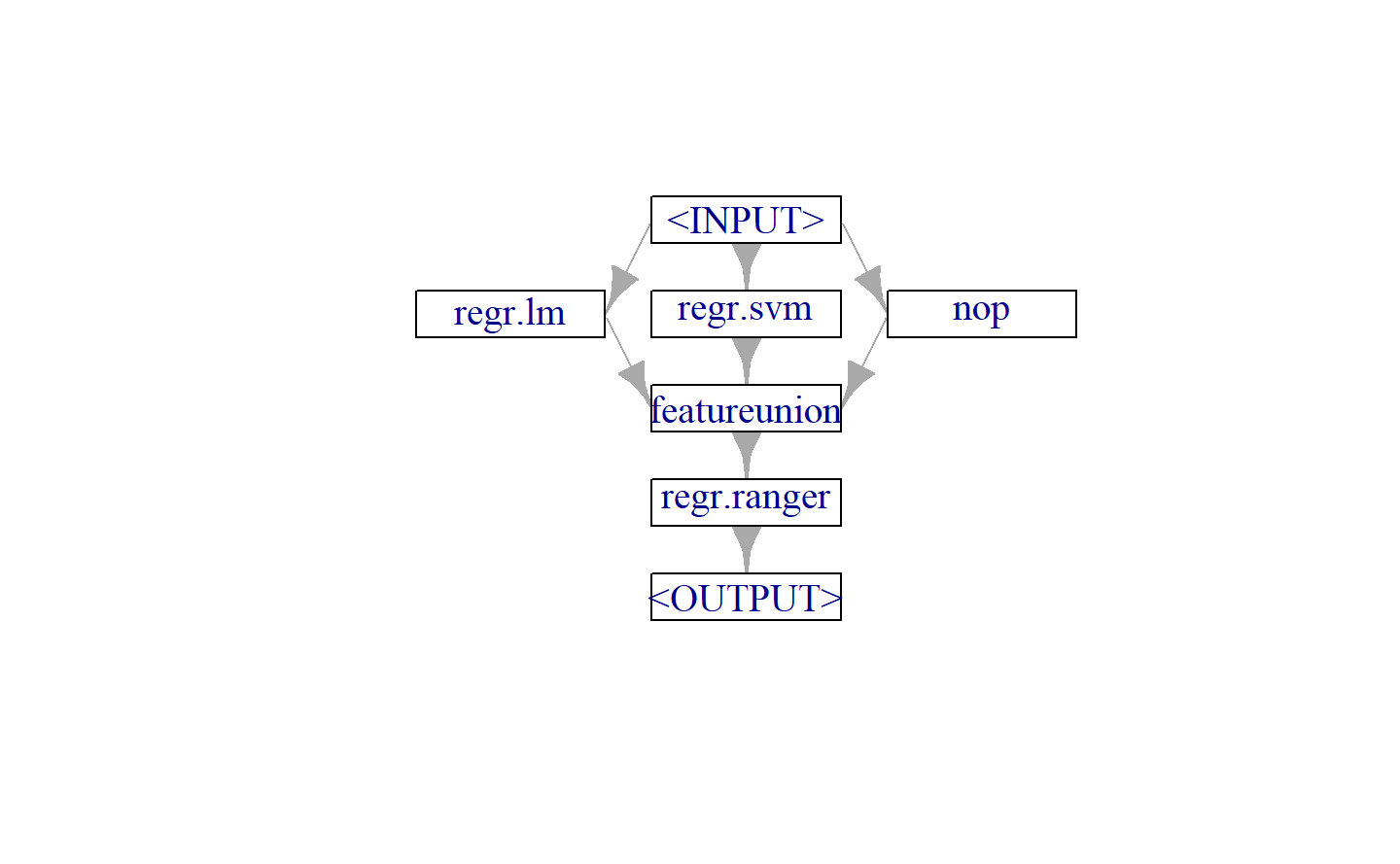

# 转为图学习器，可与普通学习器一样使用
stacklrn = as_learner(graph_stack)
stacklrn$train(tsk("mtcars"))

3 特征工程

机器学习中的数据预处理，通常也统称为特征工程，主要包括：缺失值插补、特征变换，目的是提升模型性能。

3.1 特征工程概述

用 mlr3pipelines 包实现特征工程。

# 查看所有 PipeOp
po()
#> <DictionaryPipeOp> with 64 stored values
#> Keys: boxcox, branch, chunk, classbalancing, classifavg, classweights,
#>   colapply, collapsefactors, colroles, copy, datefeatures, encode,
#>   encodeimpact, encodelmer, featureunion, filter, fixfactors, histbin,
#>   ica, imputeconstant, imputehist, imputelearner, imputemean,
#>   imputemedian, imputemode, imputeoor, imputesample, kernelpca,
#>   learner, learner_cv, missind, modelmatrix, multiplicityexply,
#>   multiplicityimply, mutate, nmf, nop, ovrsplit, ovrunite, pca, proxy,
#>   quantilebin, randomprojection, randomresponse, regravg,
#>   removeconstants, renamecolumns, replicate, scale, scalemaxabs,
#>   scalerange, select, smote, spatialsign, subsample, targetinvert,
#>   targetmutate, targettrafoscalerange, textvectorizer, threshold,
#>   tunethreshold, unbranch, vtreat, yeojohnson

gr = po("scale") %>>% po("pca", rank. = 2)
gr$plot()

特征工程管道的三种用法：

调试：查看特征工程步对输入数据做了什么

# 训练特征工程管道：提供任务，访问特征工程之后的数据
task = tsk("iris")
gr$train(task)[[1]]$data()
#>        Species        PC1         PC2
#>   1:    setosa -2.2571412 -0.47842383
#>   2:    setosa -2.0740130  0.67188269
#>   3:    setosa -2.3563351  0.34076642
#>   4:    setosa -2.2917068  0.59539986
#>   5:    setosa -2.3818627 -0.64467566
#>  ---                                 
#> 146: virginica  1.8642579 -0.38567404
#> 147: virginica  1.5593565  0.89369285
#> 148: virginica  1.5160915 -0.26817075
#> 149: virginica  1.3682042 -1.00787793
#> 150: virginica  0.9574485  0.02425043

# 将训练好的特征工程管道，用于新的数据
gr$predict(task$filter(1:5))[[1]]$data()
#>    Species       PC1        PC2
#> 1:  setosa -2.257141 -0.4784238
#> 2:  setosa -2.074013  0.6718827
#> 3:  setosa -2.356335  0.3407664
#> 4:  setosa -2.291707  0.5953999
#> 5:  setosa -2.381863 -0.6446757

用于机器学习：原始任务经过特征工程管道变成预处理之后的任务，再正常用于机器学习流程

newtask = gr$train(task)[[1]]
newtask
#> <TaskClassif:iris> (5 x 3): Iris Flowers
#> * Target: Species
#> * Properties: multiclass
#> * Features (2):
#>   - dbl (2): PC1, PC2

用于机器学习：再接一个学习器，转化成图学习器，同普通学习器一样使用，适合对特征工程步、ML 算法一起联动调参

gr = gr %>>% lrn("classif.rpart")
gr$plot()

gr_learner = as_learner(gr)
gr_learner
#> <GraphLearner:scale.pca.classif.rpart>
#> * Model: -
#> * Parameters: scale.robust=FALSE, pca.rank.=2, classif.rpart.xval=0
#> * Packages: mlr3, mlr3pipelines, rpart
#> * Predict Types:  [response], prob
#> * Feature Types: logical, integer, numeric, character, factor, ordered,
#>   POSIXct
#> * Properties: featureless, hotstart_backward, hotstart_forward,
#>   importance, loglik, missings, multiclass, oob_error,
#>   selected_features, twoclass, weights

3.2 缺失值插补

目前支持的插补方法：

as.data.table(mlr_pipeops)[tags %in% "missings", "key"]
#>               key
#> 1: imputeconstant
#> 2:     imputehist
#> 3:  imputelearner
#> 4:     imputemean
#> 5:   imputemedian
#> 6:     imputemode
#> 7:      imputeoor
#> 8:   imputesample

3.2.1 简单插补

task = tsk("pima")
task$missings()
#> diabetes      age  glucose  insulin     mass pedigree pregnant pressure 
#>        0        0        5      374       11        0        0       35 
#>  triceps 
#>      227

# 常数插补
po = po("imputeconstant", param_vals = list(
  constant = -999, affect_columns = selector_name("glucose")
))
new_task = po$train(list(task = task))[[1]]
new_task$missings()
#> diabetes      age  insulin     mass pedigree pregnant pressure  triceps 
#>        0        0      374       11        0        0       35      227 
#>  glucose 
#>        0

# 均值插补
po = po("imputemean")
new_task = po$train(list(task = task))[[1]]
new_task$missings()
#> diabetes      age pedigree pregnant  glucose  insulin     mass pressure 
#>        0        0        0        0        0        0        0        0 
#>  triceps 
#>        0

3.2.2 随机抽样插补

通过从非缺失的训练数据中随机抽样来插补特征。

po = po("imputesample")
new_task = po$train(list(task = task))[[1]]
new_task$missings()
#> diabetes      age pedigree pregnant  glucose  insulin     mass pressure 
#>        0        0        0        0        0        0        0        0 
#>  triceps 
#>        0

3.2.3 直方图法插补

po = po("imputehist")
new_task = po$train(list(task = task))[[1]]
new_task$missings()
#> diabetes      age pedigree pregnant  glucose  insulin     mass pressure 
#>        0        0        0        0        0        0        0        0 
#>  triceps 
#>        0

3.2.4 学习器插补

# 决策树插补
po = po("imputelearner", lrn("regr.rpart"))
new_task = po$train(list(task = task))[[1]]
new_task$missings()
#> diabetes      age pedigree pregnant  glucose  insulin     mass pressure 
#>        0        0        0        0        0        0        0        0 
#>  triceps 
#>        0

# KNN插补，训练KNN学习器时，先用直方图法插补
po = po("imputelearner", 
        po("imputehist") %>>% lrn("regr.kknn"))
new_task = po$train(list(task = task))[[1]]
new_task$missings()
#> diabetes      age pedigree pregnant  glucose  insulin     mass pressure 
#>        0        0        0        0        0        0        0        0 
#>  triceps 
#>        0

3.3 特征工程

3.3.1 特征缩放

不同数值型特征的数据量纲可能相差多个数量级，这对很多数据模型会有很大影响，所以有必要做归一化处理，就是将列或行对齐并转化为一致。

library(tidyverse)
df = as_tibble(iris) %>% 
  set_names(str_c("x", 1:4), "Species")
task = as_task_classif(df, target = "Species")

3.3.1.1 标准化

标准化也称为 Z 标准化，将数据变成均值为 0，标准差为 1。

pos = po("scale")  # 参数 scale = FALSE，只做中心化
pos$train(list(task))[[1]]$data()
#>        Species          x1          x2         x3         x4
#>   1:    setosa -0.89767388  1.01560199 -1.3357516 -1.3110521
#>   2:    setosa -1.13920048 -0.13153881 -1.3357516 -1.3110521
#>   3:    setosa -1.38072709  0.32731751 -1.3923993 -1.3110521
#>   4:    setosa -1.50149039  0.09788935 -1.2791040 -1.3110521
#>   5:    setosa -1.01843718  1.24503015 -1.3357516 -1.3110521
#>  ---                                                        
#> 146: virginica  1.03453895 -0.13153881  0.8168591  1.4439941
#> 147: virginica  0.55148575 -1.27867961  0.7035638  0.9192234
#> 148: virginica  0.79301235 -0.13153881  0.8168591  1.0504160
#> 149: virginica  0.43072244  0.78617383  0.9301544  1.4439941
#> 150: virginica  0.06843254 -0.13153881  0.7602115  0.7880307

注：中心化后，0 就代表均值，更方便模型解释。

3.3.1.2 归一化

归一化是将数据线性放缩到 $\left[0, 1\right]$（根据需要也可以线性放缩到 $\left[a, b\right]$）, 一般还同时考虑指标一致化，将正向指标（值越大越好）和负向指标（值越小越好）都变成正向。

正向指标：

\[ x_i'=\frac{x_i - \text{min} x_i}{\text{max} x_i - \text{min} x_i} \]

负向指标：

\[ x_i'=\frac{\text{max} x_i - x_i}{\text{max} x_i - \text{min} x_i} \]

pop = po("scalerange", param_vals = list(lower = 0, upper = 1))
pop$train(list(task))[[1]]$data()
#>        Species         x1        x2         x3         x4
#>   1:    setosa 0.22222222 0.6250000 0.06779661 0.04166667
#>   2:    setosa 0.16666667 0.4166667 0.06779661 0.04166667
#>   3:    setosa 0.11111111 0.5000000 0.05084746 0.04166667
#>   4:    setosa 0.08333333 0.4583333 0.08474576 0.04166667
#>   5:    setosa 0.19444444 0.6666667 0.06779661 0.04166667
#>  ---                                                     
#> 146: virginica 0.66666667 0.4166667 0.71186441 0.91666667
#> 147: virginica 0.55555556 0.2083333 0.67796610 0.75000000
#> 148: virginica 0.61111111 0.4166667 0.71186441 0.79166667
#> 149: virginica 0.52777778 0.5833333 0.74576271 0.91666667
#> 150: virginica 0.44444444 0.4166667 0.69491525 0.70833333

3.3.1.3 行规范化

行规范化，常用于文本数据或聚类算法，是保证每行具有单位范数，即每行的向量“长度”相同。想象一下，$m$ 个特征下，每行数据都是 $m$ 维空间中的一个点，做行规范化能让这些点都落在单位球面上（到原点的距离均为 1）。

行规范化一般采用 L2 范数：

\[ x_{ij}' = \frac{x_{ij}}{\|x_i\|} = \frac{x_{ij}}{\sqrt{\sum_{j=1}^m x_{ij}^2}} \]

pop = po("spatialsign")
pop$train(list(task))[[1]]$data()
#>        Species        x1        x2        x3         x4
#>   1:    setosa 0.8037728 0.5516088 0.2206435 0.03152050
#>   2:    setosa 0.8281329 0.5070201 0.2366094 0.03380134
#>   3:    setosa 0.8053331 0.5483119 0.2227517 0.03426949
#>   4:    setosa 0.8000302 0.5391508 0.2608794 0.03478392
#>   5:    setosa 0.7909650 0.5694948 0.2214702 0.03163860
#>  ---                                                   
#> 146: virginica 0.7215572 0.3230853 0.5600146 0.24769876
#> 147: virginica 0.7296536 0.2895451 0.5790902 0.22005426
#> 148: virginica 0.7165390 0.3307103 0.5732312 0.22047353
#> 149: virginica 0.6746707 0.3699807 0.5876164 0.25028107
#> 150: virginica 0.6902592 0.3509792 0.5966647 0.21058754

3.3.2 特征变换

3.3.2.1 非线性特征

对于数值特征 $x_1, x_2, \cdots$，可以穿件更多的多项式特征：$x_1^2, x_1, x_2^2, x2, \cdots$，这相当于是用自变量的更高阶泰勒公式去逼近因变量。

pop = po("modelmatrix", formula = ~ . ^ 2 + I(x1 ^ 2) + log(x2))
pop$train(list(task))[[1]]$data()
#>        Species (Intercept)  x1  x2  x3  x4 I(x1^2)   log(x2) x1:x2 x1:x3 x1:x4
#>   1:    setosa           1 5.1 3.5 1.4 0.2   26.01 1.2527630 17.85  7.14  1.02
#>   2:    setosa           1 4.9 3.0 1.4 0.2   24.01 1.0986123 14.70  6.86  0.98
#>   3:    setosa           1 4.7 3.2 1.3 0.2   22.09 1.1631508 15.04  6.11  0.94
#>   4:    setosa           1 4.6 3.1 1.5 0.2   21.16 1.1314021 14.26  6.90  0.92
#>   5:    setosa           1 5.0 3.6 1.4 0.2   25.00 1.2809338 18.00  7.00  1.00
#>  ---                                                                          
#> 146: virginica           1 6.7 3.0 5.2 2.3   44.89 1.0986123 20.10 34.84 15.41
#> 147: virginica           1 6.3 2.5 5.0 1.9   39.69 0.9162907 15.75 31.50 11.97
#> 148: virginica           1 6.5 3.0 5.2 2.0   42.25 1.0986123 19.50 33.80 13.00
#> 149: virginica           1 6.2 3.4 5.4 2.3   38.44 1.2237754 21.08 33.48 14.26
#> 150: virginica           1 5.9 3.0 5.1 1.8   34.81 1.0986123 17.70 30.09 10.62
#>      x2:x3 x2:x4 x3:x4
#>   1:  4.90  0.70  0.28
#>   2:  4.20  0.60  0.28
#>   3:  4.16  0.64  0.26
#>   4:  4.65  0.62  0.30
#>   5:  5.04  0.72  0.28
#>  ---                  
#> 146: 15.60  6.90 11.96
#> 147: 12.50  4.75  9.50
#> 148: 15.60  6.00 10.40
#> 149: 18.36  7.82 12.42
#> 150: 15.30  5.40  9.18

另一种常用的非线性特征是基于自然样条的样条特征（暂时没有专门的PipeOp）：

pop = po("modelmatrix", formula = ~ splines::ns(x1, 5))
pop$train(list(task))[[1]]$data()
#>        Species (Intercept) splines::ns(x1, 5)1 splines::ns(x1, 5)2
#>   1:    setosa           1        3.094150e-01        0.0009968102
#>   2:    setosa           1        1.318681e-01        0.0000000000
#>   3:    setosa           1        3.907204e-02        0.0000000000
#>   4:    setosa           1        1.648352e-02        0.0000000000
#>   5:    setosa           1        2.094017e-01        0.0000000000
#>  ---                                                              
#> 146: virginica           1        0.000000e+00        0.3024574669
#> 147: virginica           1        1.812956e-02        0.6788378608
#> 148: virginica           1        1.362101e-05        0.4802626315
#> 149: virginica           1        5.579165e-02        0.7426950594
#> 150: virginica           1        3.630706e-01        0.6033287054
#>      splines::ns(x1, 5)3 splines::ns(x1, 5)4 splines::ns(x1, 5)5
#>   1:         -0.20323541          0.46832508        -0.265089667
#>   2:         -0.21657099          0.49905488        -0.282483895
#>   3:         -0.17532519          0.40401021        -0.228685025
#>   4:         -0.13961683          0.32172574        -0.182108907
#>   5:         -0.21746675          0.50111903        -0.283652281
#>  ---                                                            
#> 146:          0.52049703          0.20822647        -0.031180964
#> 147:          0.26175304          0.08745429        -0.046174752
#> 148:          0.42721751          0.15182156        -0.059315324
#> 149:          0.17592803          0.05799882        -0.032413564
#> 150:          0.01963969          0.01354992        -0.007669769

3.3.2.2 计算新特征

管道运算“mutate”，根据以公式形式给出的表达式添加特征，这些表达式可能取决于其他特征的值。这可以增加新的特征，也可以改变现有的特征。

pom = po("mutate", mutation = list(
  x1_p = ~ x1 + 1,
  Area1 = ~ x1 * x2,
  Area2 = ~ x3 * x4,
  Area = ~ Area1 + Area2
))
pom$train(list(task))[[1]]$data()
#>        Species  x1  x2  x3  x4 x1_p Area1 Area2  Area
#>   1:    setosa 5.1 3.5 1.4 0.2  6.1 17.85  0.28 18.13
#>   2:    setosa 4.9 3.0 1.4 0.2  5.9 14.70  0.28 14.98
#>   3:    setosa 4.7 3.2 1.3 0.2  5.7 15.04  0.26 15.30
#>   4:    setosa 4.6 3.1 1.5 0.2  5.6 14.26  0.30 14.56
#>   5:    setosa 5.0 3.6 1.4 0.2  6.0 18.00  0.28 18.28
#>  ---                                                 
#> 146: virginica 6.7 3.0 5.2 2.3  7.7 20.10 11.96 32.06
#> 147: virginica 6.3 2.5 5.0 1.9  7.3 15.75  9.50 25.25
#> 148: virginica 6.5 3.0 5.2 2.0  7.5 19.50 10.40 29.90
#> 149: virginica 6.2 3.4 5.4 2.3  7.2 21.08 12.42 33.50
#> 150: virginica 5.9 3.0 5.1 1.8  6.9 17.70  9.18 26.88

利用正则表达式从复杂字符串列提取出相关信息，并转化为因子特征：

po_ftextract = po("mutate", mutation = list(
  fare_per_person = ~ fare / (parch + sib_sp + 1),
  deck = ~ factor(str_sub(cabin, 1, 1)),
  title = ~ factor(str_extract(name, "(?<=, ).*(?=\\.)")),
  surname = ~ factor(str_extract(name, "^.*(?=,)")),
  ticket_prefix = ~ factor(str_extract(ticket, "^.*(?= )"))
))
po_ftextract$train(list(tsk("titanic")))[[1]]$data()
#>       survived  age cabin embarked     fare
#>    1:       no 22.0  <NA>        S   7.2500
#>    2:      yes 38.0   C85        C  71.2833
#>    3:      yes 26.0  <NA>        S   7.9250
#>    4:      yes 35.0  C123        S  53.1000
#>    5:       no 35.0  <NA>        S   8.0500
#>   ---                                      
#> 1305:     <NA>   NA  <NA>        S   8.0500
#> 1306:     <NA> 39.0  C105        C 108.9000
#> 1307:     <NA> 38.5  <NA>        S   7.2500
#> 1308:     <NA>   NA  <NA>        S   8.0500
#> 1309:     <NA>   NA  <NA>        C  22.3583
#>                                                      name parch pclass    sex
#>    1:                             Braund, Mr. Owen Harris     0      3   male
#>    2: Cumings, Mrs. John Bradley (Florence Briggs Thayer)     0      1 female
#>    3:                              Heikkinen, Miss. Laina     0      3 female
#>    4:        Futrelle, Mrs. Jacques Heath (Lily May Peel)     0      1 female
#>    5:                            Allen, Mr. William Henry     0      3   male
#>   ---                                                                        
#> 1305:                                  Spector, Mr. Woolf     0      3   male
#> 1306:                        Oliva y Ocana, Dona. Fermina     0      1 female
#> 1307:                        Saether, Mr. Simon Sivertsen     0      3   male
#> 1308:                                 Ware, Mr. Frederick     0      3   male
#> 1309:                            Peter, Master. Michael J     1      3   male
#>       sib_sp             ticket fare_per_person deck  title       surname
#>    1:      1          A/5 21171        3.625000 <NA>     Mr        Braund
#>    2:      1           PC 17599       35.641650    C    Mrs       Cumings
#>    3:      0   STON/O2. 3101282        7.925000 <NA>   Miss     Heikkinen
#>    4:      1             113803       26.550000    C    Mrs      Futrelle
#>    5:      0             373450        8.050000 <NA>     Mr         Allen
#>   ---                                                                    
#> 1305:      0          A.5. 3236        8.050000 <NA>     Mr       Spector
#> 1306:      0           PC 17758      108.900000    C   Dona Oliva y Ocana
#> 1307:      0 SOTON/O.Q. 3101262        7.250000 <NA>     Mr       Saether
#> 1308:      0             359309        8.050000 <NA>     Mr          Ware
#> 1309:      1               2668        7.452767 <NA> Master         Peter
#>       ticket_prefix
#>    1:           A/5
#>    2:            PC
#>    3:      STON/O2.
#>    4:          <NA>
#>    5:          <NA>
#>   ---              
#> 1305:          A.5.
#> 1306:            PC
#> 1307:    SOTON/O.Q.
#> 1308:          <NA>
#> 1309:          <NA>

若数据噪声太多的问题，通常就需要做数据平滑。

pom = po("mutate", mutation = list(
  x1_s = ~ slider::slide_dbl(x1, mean, .before = 2, .after = 2) # 五点移动平均
))
dat = pom$train(list(task = task))[[1]]$data()

library(patchwork)
p1 = ggplot(dat, aes(1:150, x1)) + geom_line()
p2 = ggplot(dat, aes(1:150, x1_s)) + geom_line()
p1 / p2

# colapply：应用函数到任务的每一列，常用于类型转换
poca = po("colapply", applicator = as.character)

# renamecolumns：修改列名
pop = po("renamecolumns", param_vals = list(
  renaming = c("Petal.Length" = "PL")
))

3.3.2.3 正态性变换

Box-Cox 变换是更神奇的正态性变换，用最大似然估计选择最优的 $\lambda$ 值，让非负的非正态数据变成正态数据：

\[ y' = \begin{cases} \ln y & \lambda = 0 \\ (y^{\lambda} - 1)/ \lambda & \lambda \neq 0 \end{cases} \]

pop = po("boxcox")
pop$train(list(task))[[1]]$data()
#>        Species         x1          x2         x3         x4
#>   1:    setosa -0.8917547  1.01831791 -1.3431567 -1.3850773
#>   2:    setosa -1.1812229 -0.08167295 -1.3431567 -1.3850773
#>   3:    setosa -1.4845435  0.37307046 -1.4033413 -1.3850773
#>   4:    setosa -1.6417967  0.14833599 -1.2832670 -1.3850773
#>   5:    setosa -1.0348319  1.22454068 -1.3431567 -1.3850773
#>  ---                                                       
#> 146: virginica  1.0385560 -0.08167295  0.8174171  1.2930924
#> 147: virginica  0.6097200 -1.32264877  0.7075555  0.9020852
#> 148: virginica  0.8279148 -0.08167295  0.8174171  1.0023867
#> 149: virginica  0.4976284  0.80781419  0.9269887  1.2930924
#> 150: virginica  0.1485189 -0.08167295  0.7625234  0.7998822

若数据包含 0 或负数，则 Box-Cox 变换不再适用，可以改用同样原理的 Yeo-Johnson 变换：

\[ y' = \begin{cases} \ln (y+1) & \lambda = 0, y \geq 0\\ \frac{(y + 1)^{\lambda} - 1}{\lambda} & \lambda \neq 0, y \geq 0\\ - \ln (1-y) & \lambda = 2, y < 0\\ \frac{(1-y)^{2-\lambda} - 1}{\lambda - 2} & \lambda \neq 2, y < 0 \end{cases} \]

pop = po("yeojohnson")
pop$train(list(task))[[1]]$data()
#>        Species         x1          x2         x3         x4
#>   1:    setosa -0.8926989  1.01949272 -1.3278574 -1.3278174
#>   2:    setosa -1.1812158 -0.08164367 -1.3278574 -1.3278174
#>   3:    setosa -1.4829526  0.37387369 -1.3813346 -1.3278174
#>   4:    setosa -1.6391179  0.14878429 -1.2741721 -1.3278174
#>   5:    setosa -1.0353690  1.22553197 -1.3278574 -1.3278174
#>  ---                                                       
#> 146: virginica  1.0393000 -0.08164367  0.8157632  1.4105911
#> 147: virginica  0.6095086 -1.32389503  0.6988626  0.9184998
#> 148: virginica  0.8281903 -0.08164367  0.8157632  1.0424849
#> 149: virginica  0.4971768  0.80900587  0.9330158  1.4105911
#> 150: virginica  0.1474204 -0.08164367  0.7572682  0.7938307

3.3.2.4 连续变量分箱

在统计和机器学习中，有时需要将连续变量转化为离散变量，称为连续变量离散化或分箱，常用于银行风控建模，特别是线性回归或 Logistic 回归模型。

分箱的好处有：

使得结果更便于分析和解释。比如，年龄从中年到老年，患高血压比例增加25%，而年龄每增加一岁，患高血压比例不一定有显著变化；
简化模型，将自变量与因变量间非线性的潜在的关系，转化为简单的线性关系。当然，分箱也可能带来问题：简化的模型关系可能与潜在的模型关系不一致（甚至发现的是错误的模型关系）、删除数据中的细微差别、切分点可能没有实际意义。

# 等宽分箱
pop = po("histbin", param_vals = list(breaks = 4))
pop$train(list(task))[[1]]$data()
#>        Species       x1         x2       x3         x4
#>   1:    setosa    (5,6]    (3,3.5] [-Inf,2] [-Inf,0.5]
#>   2:    setosa [-Inf,5]    (2.5,3] [-Inf,2] [-Inf,0.5]
#>   3:    setosa [-Inf,5]    (3,3.5] [-Inf,2] [-Inf,0.5]
#>   4:    setosa [-Inf,5]    (3,3.5] [-Inf,2] [-Inf,0.5]
#>   5:    setosa [-Inf,5]    (3.5,4] [-Inf,2] [-Inf,0.5]
#>  ---                                                  
#> 146: virginica    (6,7]    (2.5,3]    (4,6]   (2, Inf]
#> 147: virginica    (6,7] [-Inf,2.5]    (4,6]    (1.5,2]
#> 148: virginica    (6,7]    (2.5,3]    (4,6]    (1.5,2]
#> 149: virginica    (6,7]    (3,3.5]    (4,6]   (2, Inf]
#> 150: virginica    (5,6]    (2.5,3]    (4,6]    (1.5,2]

# 分位数分箱
pop = po("quantilebin", numsplits = 4)
pop$train(list(task))[[1]]$data()
#>        Species         x1         x2         x3         x4
#>   1:    setosa (-Inf,5.1] (3.3, Inf] (-Inf,1.6] (-Inf,0.3]
#>   2:    setosa (-Inf,5.1]    (2.8,3] (-Inf,1.6] (-Inf,0.3]
#>   3:    setosa (-Inf,5.1]    (3,3.3] (-Inf,1.6] (-Inf,0.3]
#>   4:    setosa (-Inf,5.1]    (3,3.3] (-Inf,1.6] (-Inf,0.3]
#>   5:    setosa (-Inf,5.1] (3.3, Inf] (-Inf,1.6] (-Inf,0.3]
#>  ---                                                      
#> 146: virginica (6.4, Inf]    (2.8,3] (5.1, Inf] (1.8, Inf]
#> 147: virginica  (5.8,6.4] (-Inf,2.8] (4.35,5.1] (1.8, Inf]
#> 148: virginica (6.4, Inf]    (2.8,3] (5.1, Inf] (1.8, Inf]
#> 149: virginica  (5.8,6.4] (3.3, Inf] (5.1, Inf] (1.8, Inf]
#> 150: virginica  (5.8,6.4]    (2.8,3] (4.35,5.1]  (1.3,1.8]

3.3.3 特征降维

有时数据集可能包含过多特征，甚至是冗余特征，可以用降维技术进压缩特征，但通常会降低模型性能。

3.3.3.1 PCA

$n$ 个特征，若转化为 $n$ 个主成分，则会保留原始数据的 100% 信息，但这就失去了降维的意义。所以1一般是只选择前若干个主成分，一般原则是选择至保留 85% 以上信息的主成分。

pop = po("pca", rank. = 2)
pop$train(list(task))[[1]]$data()
#>        Species       PC1         PC2
#>   1:    setosa -2.684126 -0.31939725
#>   2:    setosa -2.714142  0.17700123
#>   3:    setosa -2.888991  0.14494943
#>   4:    setosa -2.745343  0.31829898
#>   5:    setosa -2.728717 -0.32675451
#>  ---                                
#> 146: virginica  1.944110 -0.18753230
#> 147: virginica  1.527167  0.37531698
#> 148: virginica  1.764346 -0.07885885
#> 149: virginica  1.900942 -0.11662796
#> 150: virginica  1.390189  0.28266094

3.3.3.2 核 PCA

PCA 适用于数据的线性降维。而核主成分分析（Kernel PCA, KPCA）可实现数据的非线性降维，用于处理线性不可分的数据集。

KPCA 的大致思路是：对于输入空间中的矩阵 $X$，先用一个非线性映射把 $X$ 中的所有样本映射到一个高维甚至是无穷维的特征空间（使其线性可分），然后在这个高维空间进行 PCA 降维。

3.3.3.3 ICA：独立成分分析

独立成分分析，提取统计意义上的独立成分：

pop = po("ica", n.comp = 3)
pop$train(list(task))[[1]]$data()
#>        Species         V1         V2         V3
#>   1:    setosa  0.1721410  0.4149772 -1.3952557
#>   2:    setosa  0.2214486 -0.7872973 -1.3361069
#>   3:    setosa -0.4563409 -0.3146524 -1.3308693
#>   4:    setosa -0.6610660 -0.5861230 -1.2029337
#>   5:    setosa -0.1833669  0.6446961 -1.3678177
#>  ---                                           
#> 146: virginica -0.1793776  0.7197010  0.9500885
#> 147: virginica  0.1249361 -0.8278466  0.7937129
#> 148: virginica -0.1614076  0.4371009  0.8769270
#> 149: virginica -1.9147519  1.6044931  1.1871656
#> 150: virginica -1.2683559  0.2261212  0.9094067

3.3.3.4 NMF：非负矩阵分解

对于任意给定的非负矩阵 $V$，NMF 算法能够寻找到非负矩阵 $W$ 和非负矩阵 $H$，使它们的积为矩阵。非负矩阵分解的方法在保证矩阵的非负性的同时能够减少数据量，相当于把 $n$ 维的数据降维到 $r$ 维。

# BiocManager::install("Biobase")
pop = po("nmf", rank = 3)
pop$train(list(task))[[1]]$data()
#> Registered S3 methods overwritten by 'registry':
#>   method               from 
#>   print.registry_field proxy
#>   print.registry_entry proxy
#>        Species       NMF1      NMF2         NMF3
#>   1:    setosa 0.08946447 0.4806157  0.039331051
#>   2:    setosa 0.14847785 0.4012262 -0.003756253
#>   3:    setosa 0.08482244 0.4394040  0.037395481
#>   4:    setosa 0.10090716 0.4121730  0.052304626
#>   5:    setosa 0.06054158 0.4968302  0.064062112
#>  ---                                            
#> 146: virginica 0.26134716 0.3282638  0.600819824
#> 147: virginica 0.34676264 0.2323164  0.469663330
#> 148: virginica 0.28374883 0.3073426  0.552988371
#> 149: virginica 0.14504617 0.3818651  0.727874559
#> 150: virginica 0.23580629 0.3002660  0.566502348

3.3.3.5 剔除常量特征

从任务中剔除常量特征。对于每个特征，计算不同于其众数值的比例。所有比例低于可设置阈值的特征都会从任务中剔除。缺失值可以被忽略，也可以视为与非缺失值不同的常规值。

data = data.table(y = runif(10), a = 1:10, b = rep(1, 10), 
                  c = rep(1:2, each = 5))
task_ex = as_task_regr(data, target = "y")
po = po("removeconstants")  # 剔除常量特征 b
po$train(list(task_ex))[[1]]$data()
#>               y  a c
#>  1: 0.891268901  1 1
#>  2: 0.002797802  2 1
#>  3: 0.649207745  3 1
#>  4: 0.561067845  4 1
#>  5: 0.427392408  5 1
#>  6: 0.387362043  6 2
#>  7: 0.544585730  7 2
#>  8: 0.622006226  8 2
#>  9: 0.183312478  9 2
#> 10: 0.342760530 10 2

3.3.4 分类特征

3.3.4.1 因子折叠

管道运算“collapsefactors”，对因子或有序因子进行折叠，折叠训练样本中最少的水平，直到剩下 target_level_count 个水平。然而，那些出现率高于 no_collapse_above_prevalence 的水平会被保留。对于因子变量，它们被折叠到下一个更大的水平，对于有序变量，稀有变量被折叠到相邻的类别，以样本数较少者为准。

训练集中没有出现的水平在预测集中不会被使用，因此经常与因子修正结合起来使用。

dat = tibble(color = factor(starwars$skin_color), y = 1)
dat %>% count(color)
#> # A tibble: 31 × 2
#>    color                   n
#>    <fct>               <int>
#>  1 blue                    2
#>  2 blue, grey              2
#>  3 brown                   4
#>  4 brown mottle            1
#>  5 brown, white            1
#>  6 dark                    6
#>  7 fair                   17
#>  8 fair, green, yellow     1
#>  9 gold                    1
#> 10 green                   6
#> # ℹ 21 more rows

task = as_task_regr(dat, target = "y")
poc = po("collapsefactors", target_level_count = 5)
poc$train(list(task))[[1]]$data() %>% count(color)
#>    color  n
#> 1:  dark  6
#> 2:  fair 17
#> 3: green  6
#> 4:  grey 47
#> 5: light 11

3.3.4.2 因子修正

管道运算“fixfactors”（参数：droplevels = TRUE）确保预测过程中的因子水平与训练过程中的相同；可能会在之前丢弃空的训练因子水平。

注意，如果发现未见过的因子水平，这可能会在预测期间引入缺失值。

dattrain = data.table(
  a = factor(c("a", "b", "c", NA), levels = letters),
  b = ordered(c("a", "b", "c", NA)),
  target = 1:4
)
dattrain
#>       a    b target
#> 1:    a    a      1
#> 2:    b    b      2
#> 3:    c    c      3
#> 4: <NA> <NA>      4

dattest = data.table(
  a = factor(c("a", "b", "c", "d"), levels = letters[10:1]),
  b = ordered(c("a", "b", "c", "d")),
  target = 1:4
)
dattest
#>    a b target
#> 1: a a      1
#> 2: b b      2
#> 3: c c      3
#> 4: d d      4

task_train = as_task_regr(dattrain, "target")
task_test = as_task_regr(dattest, "target")
po = po("fixfactors")
po$train(list(task_train))
#> $output
#> <TaskRegr:dattrain> (4 x 3)
#> * Target: target
#> * Properties: -
#> * Features (2):
#>   - fct (1): a
#>   - ord (1): b

po$predict(list(task_test))[[1]]$data()
#>    target    a    b
#> 1:      1    a    a
#> 2:      2    b    b
#> 3:      3    c    c
#> 4:      4 <NA> <NA>

3.3.4.3 因子编码

对因子、有序因子、字符特征进行编码。参数 method 指定编码方法：

“one-hot”：独热编码；
“treatment”：虚拟编码，创建 $n-1$ 列，留出每个因子变量的第一个因子水平（见stats::conc.treatment()）；
“helmert”：根据 Helmert 对比度创建列（见stats::conc.helmert()）；
“poly”：根据正交多项式创建对比列（见stats::conc.poly()）；
“sum”：创建对比度相加为零的列，（见stats::conc.sum()）

新创建的列按模式 [column-name].[x] 命名，其中 x 是 ”one-hot” 和 ”treatment” 编码的各自因子水平，否则是一个整数序列。

task = tsk("penguins")
poe = po("encode", method = "one-hot")   # 独热编码
poe$train(list(task))[[1]]$data()[, 7:11]
#>      island.Biscoe island.Dream island.Torgersen sex.female sex.male
#>   1:             0            0                1          0        1
#>   2:             0            0                1          1        0
#>   3:             0            0                1          1        0
#>   4:             0            0                1         NA       NA
#>   5:             0            0                1          1        0
#>  ---                                                                
#> 340:             0            1                0          0        1
#> 341:             0            1                0          1        0
#> 342:             0            1                0          0        1
#> 343:             0            1                0          0        1
#> 344:             0            1                0          1        0

poe = po("encode", method = "treatment")  # 虚拟编码
poe$train(list(task))[[1]]$data()[, 7:9]
#>      island.Dream island.Torgersen sex.male
#>   1:            0                1        1
#>   2:            0                1        0
#>   3:            0                1        0
#>   4:            0                1       NA
#>   5:            0                1        0
#>  ---                                       
#> 340:            1                0        1
#> 341:            1                0        0
#> 342:            1                0        1
#> 343:            1                0        1
#> 344:            1                0        0

poe = po("encode", method = "helmert")  # Helmert 编码
poe$train(list(task))[[1]]$data()[, 7:9]
#>      island.1 island.2 sex.1
#>   1:        0        2     1
#>   2:        0        2    -1
#>   3:        0        2    -1
#>   4:        0        2    NA
#>   5:        0        2    -1
#>  ---                        
#> 340:        1       -1     1
#> 341:        1       -1    -1
#> 342:        1       -1     1
#> 343:        1       -1     1
#> 344:        1       -1    -1

poe = po("encode", method = "poly")  # 多项编码
poe$train(list(task))[[1]]$data()[, 7:9]
#>           island.1   island.2      sex.1
#>   1:  7.071068e-01  0.4082483  0.7071068
#>   2:  7.071068e-01  0.4082483 -0.7071068
#>   3:  7.071068e-01  0.4082483 -0.7071068
#>   4:  7.071068e-01  0.4082483         NA
#>   5:  7.071068e-01  0.4082483 -0.7071068
#>  ---                                    
#> 340: -7.850462e-17 -0.8164966  0.7071068
#> 341: -7.850462e-17 -0.8164966 -0.7071068
#> 342: -7.850462e-17 -0.8164966  0.7071068
#> 343: -7.850462e-17 -0.8164966  0.7071068
#> 344: -7.850462e-17 -0.8164966 -0.7071068

poe = po("encode", method = "sum")  # sum 编码
poe$train(list(task))[[1]]$data()[, 7:9]
#>      island.1 island.2 sex.1
#>   1:       -1       -1    -1
#>   2:       -1       -1     1
#>   3:       -1       -1     1
#>   4:       -1       -1    NA
#>   5:       -1       -1     1
#>  ---                        
#> 340:        0        1    -1
#> 341:        0        1     1
#> 342:        0        1    -1
#> 343:        0        1    -1
#> 344:        0        1     1

Warning

以下内容暂缓：

效应编码
日期时间特征
文本特征

3.3.5 处理不均衡数据

通过采样对任务进行类平衡，可能有利于对不平衡的训练数据进行分类，采样只发生在训练阶段。

3.3.5.1 欠采样与过采样

欠采样：只保留多数类的一部分行；过采样：对少数类进行超量采样（重复数据点）。

PipeOp 名字为 ”classbalancing”，参数：

ratio：相对于 $reference 值，要保留的类的行数的比率，默认为 1；
reference：$ratio 的值是根据什么来衡量的。可以是 “all”（默认值，所有类的平均实例数），“major”（拥有最多实例的类的实例数），“minor”（拥有最少实例的类的实例数），“nonmajor”（除主要类外所有类的平均实例数），“nonminor”（除次要类外所有类的平均实例数），以及 “one”（$ratio 决定每个类的实例数）；
adjust：哪些类要向上/向下采样。可以是 “all”（默认）、“major”、“minor”、“nonmajor”、“nonminor”、“upsample”（只过采样）和“downsample”（只欠采样）；
shuffle：是否对结果任务的行进行洗牌，默认为 TRUE。如果数据被过采样且 shuffle = FALSE，结果任务将以原始顺序显示原始行（在欠采样中不被移除），然后是所有新添加的行，按目标类别排序。

过/欠采样的过程如下：

首先，计算” 目标类计数”，方法是取 reference 参数所指示的所有类的平均数（例如，如果 reference 参数是 ”nonmajor”：所有不是 “major” 类的类的平均数，即拥有最多样本的类），然后将其与比率参数的值相乘。如果 reference 是 ”one”，那么“目标类计数” 就是比率的值（即 1 * 比率）。
然后，对于每个被 adjust 参数引用的类（例如，若调整是“nonminor”：每个不是样本最少的类），PipeOpClassBalancing 要么抛出样本（欠采样），要么增加与随机选择的样本相等的额外行（过采样），直到这些类的样本数等于“目标类计数”。
使用 task$filter() 来删除行。当在过采样过程中添加相同的行时，那么由于[混淆]，不能使用 task$row_roles$use 来复制行；而是使用 task$rbind() 函数，并附加一个新的 data.table，其中包含所有被复制的行，其次数正好与被添加的行相同。

task = tsk("german_credit")
table(task$truth())
#> 
#> good  bad 
#>  700  300

## 欠采样
opb_down = po("classbalancing", reference = "minor", adjust = "major")
# 默认ratio = 1, 若ratio = 2, 结果是600 good, 300 bad
result = opb_down$train(list(task))[[1]]
table(result$truth())
#> 
#> good  bad 
#>  300  300

## 过采样
opb_up = po("classbalancing", reference = "major", adjust = "minor")
# 默认ratio = 1, 若ratio = 2, 结果是700 good, 1400 bad
result = opb_up$train(list(task))[[1]]
table(result$truth())
#> 
#> good  bad 
#>  700  700

3.3.5.2 SMOTE 法

用 SMOTE 算法创建少数类别的合成观测，生成一个更平衡的数据集。该算法为每个少数类观测取样，基于该观测的 $K$ 个最近邻居生成新观测。它只能应用于具有纯数值特征的任务。详见 smotefamily::SMOTE。

PipeOp 名字：“smote”，其参数（具体参阅 SMOTE()）：

K：用于抽取新值的近邻的数量；
dup_size：合成的少数实例在原始多数实例数量上的期望次数。

# 只支持double 型特征, 需安装 smotefamily 包
pop = po("colapply", applicator = as.numeric,
         affect_columns = selector_type("integer")) %>>%
  po("encodeimpact") %>>%
  po("smote", K = 5, dup_size = 1)  # 少数类增加 1 倍
result = pop$train(task)[[1]]
table(result$truth())
#> 
#> good  bad 
#>  700  600

3.3.6 目标变换

为了提高预测能力，对于异方差或右偏的因变量数据，经常需要做取对数变换、或 Box-Cox 变换，以变成正态数据，再进行回归建模，预测值要回到原数据量级，还要做逆变换。

mlr3pipelines 包还提供了目标变换管道，将目标变换及其逆变换，都封装到图学习器，这样就省了手动做两次变换，还能整体进行调参或基准测试。

对于方差逐渐变大的异方差的时间序列数据，或右偏分布的数据，可以尝试做对数变换或开平方变换，以稳定方差和变成正态分布。

对数变换特别有用，因为具有可解释性：对数值的变化是原始尺度上的相对（百分比）变化。若使用以 10 为底的对数，则对数刻度上每增加 1 对应原始刻度上的乘以 10。

注意，原始数据若存在零或负，则不能取对数或开根号，解决办法是做平移：$a = \max \{ 0, -\min \{x_i\} + \varepsilon \}$

task = tsk("mtcars")
learner = lrn("regr.lm")
g_ppl = ppl("targettrafo", graph = learner)
g_ppl$param_set$values$targetmutate.trafo = function(x) log(x)
g_ppl$param_set$values$targetmutate.inverter = function(x) list(response = exp(x$response))
g_ppl$plot()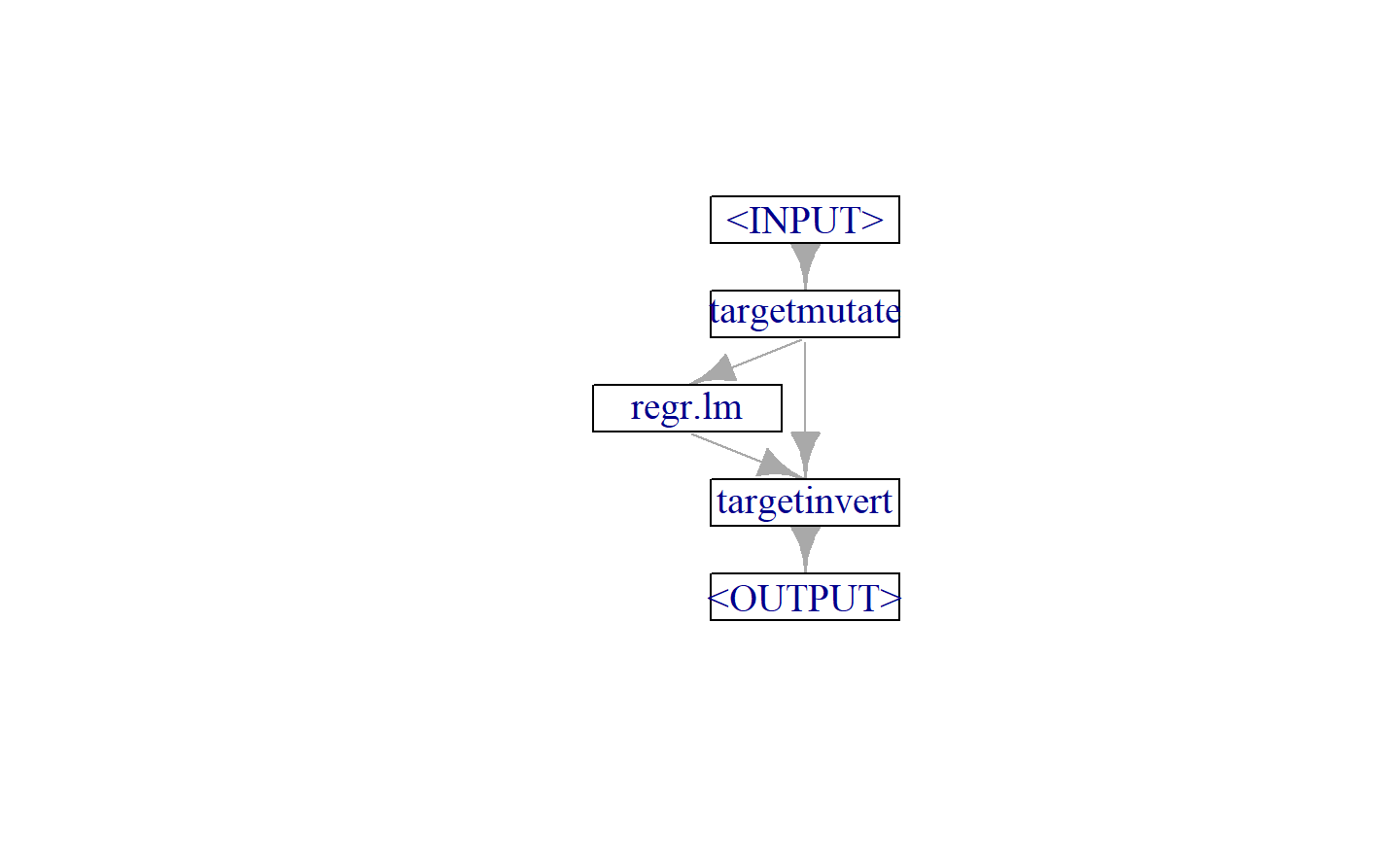

gl = as_learner(g_ppl)
gl$train(task)
gl$predict(task)
#> <PredictionRegr> for 32 observations:
#>     row_ids truth response
#>           1  21.0 21.67976
#>           2  21.0 21.10831
#>           3  22.8 25.73690
#> ---                       
#>          30  19.7 19.58533
#>          31  15.0 14.11015
#>          32  21.4 23.11105

4 嵌套重抽样

构建模型，是如何从一组潜在的候选模型（如不同的算法，不同的超参数，不同的特征子集）中选择最佳模型。在构建模型过程中所使用的重抽样划分，不应该原样用来评估最终选择模型的性能。

通过在相同的测试集或相同的 CV 划分上反复评估学习器，测试集的信息会“泄露”到评估中，导致最终的性能估计偏于乐观。

模型构建的所有部分（包括模型选择、预处理）都应该纳入到训练数据的模型寻找过程中。测试集应该只使用一次，测试集只有在模型完全训练好之后才能被使用，例如已确定好了超参数。这样从测试集获得的性能才是真实性能的无偏估计。

对于本身需要重抽样的步骤（如超参数调参），这需要两个嵌套的重抽样循环，即内层调参和外层评估都需要重抽样策略。

下面从实例来看：

使用3 折交叉验证来获得不同的非测试集和测试集（外层重抽样）
在非测试集上使用 4 折交叉验证来获得不同的内层训练集和内层测试集（内层重抽样）
使用内层数据划分来做超参数调参
使用经过内层重抽样调参的最优超参数在外层非测试集上拟合学习器
评估学习器在外层测试集上的性能
对外层重抽样的三折中的每一折重复执行 2 - 5
三个性能值被汇总为一个无偏的性能估计

过程看起来复杂，实现非常简单，只需要将内层重抽样放在自动调参器，外层重抽样放在 resample() 中，其中的学习器换成自动调参器。

# 内层重抽样（超参数调参）
at = auto_tuner(
  tuner = tnr("grid_search", resolution = 10),
  learner = lrn("classif.rpart", cp = to_tune(lower = .001, upper = .1)),
  resampling = rsmp("cv", folds = 4),
  measure = msr("classif.acc"),
  term_evals = 5
)

# 外层重抽样
task = tsk("pima")
outer_resampling = rsmp("cv", folds = 3)
rr = resample(task, at, outer_resampling, store_models = TRUE)

# 提取内层重抽样结果，查看最优的超参数
extract_inner_tuning_results(rr)
#>    iteration    cp classif.acc learner_param_vals  x_domain task_id
#> 1:         1 0.067   0.7480469          <list[2]> <list[1]>    pima
#> 2:         2 0.012   0.7578125          <list[2]> <list[1]>    pima
#> 3:         3 0.012   0.7343750          <list[2]> <list[1]>    pima
#>             learner_id resampling_id
#> 1: classif.rpart.tuned            cv
#> 2: classif.rpart.tuned            cv
#> 3: classif.rpart.tuned            cv

# 查看外层重抽样的每次结果
rr$score()
#>    task_id          learner_id resampling_id iteration classif.ce
#> 1:    pima classif.rpart.tuned            cv         1  0.2968750
#> 2:    pima classif.rpart.tuned            cv         2  0.2695312
#> 3:    pima classif.rpart.tuned            cv         3  0.2578125
#> Hidden columns: task, learner, resampling, prediction

# 查看外层重抽样的平均模型性能
rr$aggregate()
#> classif.ce 
#>  0.2747396

# 用全部数据自动调参，预测新数据
at$train(task)
dat = task$data()[1:5, -1]
at$predict_newdata(dat)

# 若改用tune_nested() 函数，嵌套重抽样过程还可以进一步简化
rr = tune_nested(
  tuner = tnr("grid_search", resolution = 10),
  task = task,
  learner = lrn("classif.rpart", cp = to_tune(lower = .001, upper = .1)),
  inner_resampling = rsmp("cv", folds = 4),
  outer_resampling = rsmp("cv", folds = 3),
  measure = msr("classif.acc"),
  term_evals = 5
)

5 超参数调参

机器学习的模型参数是模型的一阶（直接）参数，是训练模型时用梯度下降法寻优的参数，比如正则化回归模型的回归系数；而超参数是模型的二阶参数，需要事先设定为某值，才能开始训练一阶模型参数，比如正则化回归模型的惩罚参数、KNN 的邻居数等。

超参数会对所训练模型的性能产生重大影响，所以不能是随便或凭经验随便指定，而是需要设定很多种备选配置，从中选出让模型性能最优的超参数配置，这就是超参数调参。

超参数调参是用 mlr3tuning 包实现，是一项多方联动的系统工作，需要设定：搜索空间、学习器、任务、重抽样策略、模型性能度量指标、终止条件。

learner = lrn("classif.svm")
learner$param_set  # 查看学习器的超参数
#> <ParamSet>
#>                id    class lower upper nlevels          default parents value
#>  1:     cachesize ParamDbl  -Inf   Inf     Inf               40              
#>  2: class.weights ParamUty    NA    NA     Inf                               
#>  3:         coef0 ParamDbl  -Inf   Inf     Inf                0  kernel      
#>  4:          cost ParamDbl     0   Inf     Inf                1    type      
#>  5:         cross ParamInt     0   Inf     Inf                0              
#> ---                                                                          
#> 12:            nu ParamDbl  -Inf   Inf     Inf              0.5    type      
#> 13:         scale ParamUty    NA    NA     Inf             TRUE              
#> 14:     shrinking ParamLgl    NA    NA       2             TRUE              
#> 15:     tolerance ParamDbl     0   Inf     Inf            0.001              
#> 16:          type ParamFct    NA    NA       2 C-classification

5.1 独立调参

适合传统的机器学习套路：将数据集按留出法重抽样划分为训练集和测试集，在训练集上做内层重抽样，多次“训练集拟合模型+ 验证集评估性能”，根据平均性能选出最优超参数。

选取任务，划分数据集，将测试集索引设置为留出

task = tsk("iris")
split = partition(task, ratio = .8)
task$set_row_roles(split$test, "holdout")

选择学习器，同时指定部分超参数，需要调参的超参数用 to_tune() 设定搜索范围：

learner = lrn("classif.svm", type = "C-classification", kernel = "radial",
              cost = to_tune(.1, 10), gamma = to_tune(0, 5))

用 tune() 对学习器做超参数调参，需要设定（有些是可选）：

instance = tune(
  tuner = tnr("grid_search", batch_size = 5),
  task = task,
  learner = learner,
  resampling = rsmp("cv", folds = 5),
  measures = msr("classif.ce")
)

提取超参数调参结果

instance$result
#>    cost     gamma learner_param_vals  x_domain classif.ce
#> 1:  5.6 0.5555556          <list[4]> <list[2]> 0.03333333

instance$archive  # 调参档案

autoplot(instance, type = "surface", cols_x = c("cost", "gamma"))

用最优超参数更新学习器参数，在训练集上训练模型，在测试集上做预测

learner$param_set$values = instance$result_learner_param_vals
learner$train(task)
predictions = learner$predict(task, row_ids = split$test)
predictions
#> <PredictionClassif> for 30 observations:
#>     row_ids     truth  response
#>           5    setosa    setosa
#>          13    setosa    setosa
#>          15    setosa    setosa
#> ---                            
#>         142 virginica virginica
#>         144 virginica virginica
#>         146 virginica virginica

5.2 自动调参器

上述独立调参有两个不足：

调参得到的最优超参数需要手动更新到学习器；
不方便实现嵌套重抽样。

自动调参器可以弥补上述不足，AutoTuner 是将超参数调参与学习器封装到一起，能实现自动调参的过程，并且可以像其他学习器一样使用。

创建任务、选择学习器

task = tsk("iris")
learner = lrn("classif.svm", type = "C-classification", kernel = "radial")

用 ps() 生成搜索空间，用 auto_tuner() 创建自动调参器，注意：不需要提供任务，其它参数与独立调参的 tune() 基本一样：

search_space = ps(cost = p_dbl(0.1, 10), gamma = p_int(0, 5))
at = auto_tuner(
  tuner = tnr("grid_search"),
  learner = learner,
  search_space = search_space,
  resampling = rsmp("cv", folds = 5),
  measure = msr("classif.ce")
)

外层采用 4 折交叉验证重抽样，设置 store_models = TRUE 保存每次的模型：

rr = resample(task, at, rsmp("cv", folds = 4), store_models = TRUE)

这就是执行嵌套重抽样，外层（整体拟合模型+ 评估）循环 4 次，每次内层（超参数调参）循环 5 次。

查看结果：

rr$aggregate()  # 总的平均模型性能, 也可以提供其它度量
#> classif.ce 
#> 0.06009957
rr$score()      # 外层 4 次迭代的每次结果
#>    task_id        learner_id resampling_id iteration classif.ce
#> 1:    iris classif.svm.tuned            cv         1 0.07894737
#> 2:    iris classif.svm.tuned            cv         2 0.02631579
#> 3:    iris classif.svm.tuned            cv         3 0.05405405
#> 4:    iris classif.svm.tuned            cv         4 0.08108108
#> Hidden columns: task, learner, resampling, prediction
extract_inner_tuning_results(rr)  # 内层每次的调参结果
#>    iteration cost gamma classif.ce learner_param_vals  x_domain task_id
#> 1:         1 10.0     1 0.04505929          <list[4]> <list[2]>    iris
#> 2:         2  1.2     1 0.05375494          <list[4]> <list[2]>    iris
#> 3:         3  2.3     3 0.04466403          <list[4]> <list[2]>    iris
#> 4:         4  8.9     1 0.05335968          <list[4]> <list[2]>    iris
#>           learner_id resampling_id
#> 1: classif.svm.tuned            cv
#> 2: classif.svm.tuned            cv
#> 3: classif.svm.tuned            cv
#> 4: classif.svm.tuned            cv

extract_inner_tuning_archives(rr) # 内层调参档案

在全部数据上自动调参，预测新数据

at$train(task)
dat = task$data()[1:5, -1]
at$predict_newdata(dat)

注：调参结束后，也可以取出最优超参数，更新学习器参数：

learner$param_set$values = at$tuning_result$learner_param_vals[[1]]

或者按最优超参数重新创建学习器。

另外，上述的“自动调参+ 外层重抽样”，若改用嵌套调参 tune_nested() 实现，代码会更加简洁：

rr = tune_nested(
  tuner = tnr("grid_search"),
  task = task,
  learner = learner,
  search_space = search_space,
  inner_resampling = rsmp("cv", folds = 5),
  outer_resampling = rsmp("cv", folds = 4),
  measure = msr("classif.ce")
)

5.3 定制搜索空间

用 ps() 创建搜索空间，它支持 5 种超参数类型构建：

p_dbl()：实值型（double）
p_int()：整数型
p_fct()：离散型（factor）
p_lgl()：逻辑性
p_uty()：Untyped

search_space = ps(cost = p_dbl(.1, 10),
                  kernel = p_fct(c("polynomial", "radial")))

5.3.1 变换

对于数值型超参数，在调参时经常希望前期的点比后期的点更密集一些。这可以通过对数-指数变换来实现，这也适用于大范围搜索空间。

tibble(x = 1:20,
       y = exp(seq(log(3), log(50), length.out = 20))) %>% 
  ggplot(aes(x, y)) +
  geom_point()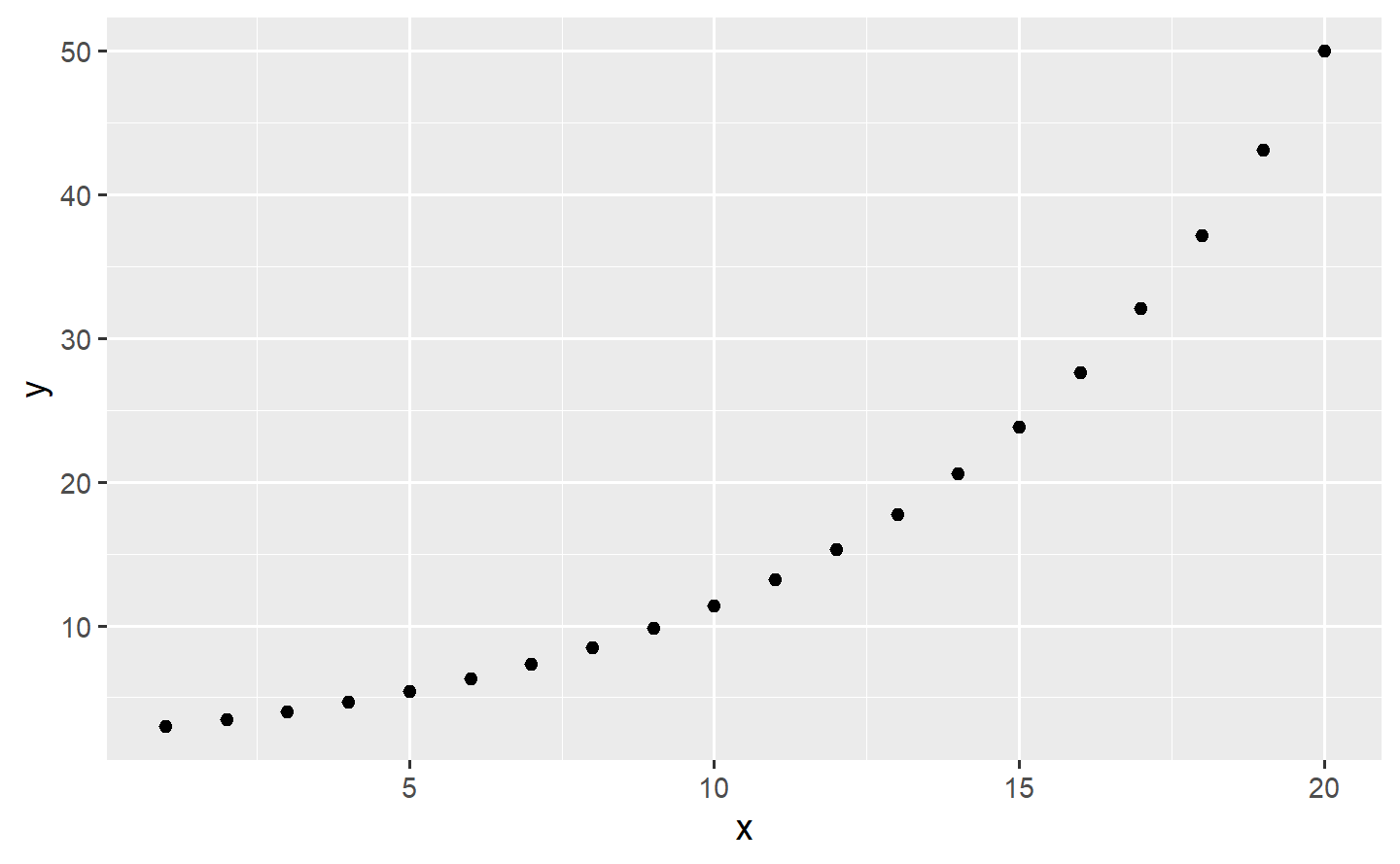

当 $x$ 均匀变化时，变换后作为超参数能前密后疏。

search_space = ps(
  cost = p_dbl(log(.1), log(10), trafo = \(x) exp(x)),
  kernel = p_fct(c("polynomial", "radial"))
)

# 查看调参网格
params = generate_design_grid(search_space, resolution = 5)
params
#> <Design> with 10 rows:
#>              cost     kernel
#>  1: -2.302585e+00 polynomial
#>  2: -2.302585e+00     radial
#>  3: -1.151293e+00 polynomial
#>  4: -1.151293e+00     radial
#>  5:  2.220446e-16 polynomial
#>  6:  2.220446e-16     radial
#>  7:  1.151293e+00 polynomial
#>  8:  1.151293e+00     radial
#>  9:  2.302585e+00 polynomial
#> 10:  2.302585e+00     radial

5.3.2 依赖关系

有些超参数只有在另一个参数取某些值时才有意义。例如，支持向量机有一个 degree 参数，只有在 kernel 为 ”polynomial” 时才有效。这可以用 depends 参数来指定：

search_space = ps(
  cost = p_dbl(log(.1), log(10), trafo = \(x) exp(x)),
  kernel = p_fct(c("polynomial", "radial")),
  degree = p_int(1, 3, depends = kernel == "polynomial")
)

5.3.3 图学习器调参

图学习器一旦成功创建，就可以像普通学习器一样使用，超参数调参时，原算法的超参数名字都自动带了学习器名字前缀，另外还可以对管道参数调参。

task = tsk("pima")

该任务包含缺失值，还有若干因子特征，都需要做预处理：插补和特征工程。

prep = gunion(list(
  po("imputehist"),
  po("missind", affect_columns = selector_type(c("numeric", "integer")))
)) %>>%
  po("featureunion") %>>%
  po("encode") %>>%
  po("removeconstants")

选择三个学习器：KNN、SVM、Ranger 作为三分支分别拟合模型，再合并分支保证是一个输出结果：

learners = list(
  knn = lrn("classif.kknn", id = "kknn"),
  svm = lrn("classif.svm", id = "svm", type = "C-classification"),
  rf = lrn("classif.ranger", id = "ranger")
)
graph = ppl("branch", learners)

将预处理图和算法图连接得到整个图，并可视化图：

graph = prep %>>% graph
graph$plot()

转化为图学习器，查看其超参数：

glearner = as_learner(graph)
glearner$param_set
#> <ParamSetCollection>
#>                            id    class lower upper nlevels          default
#>  1:          branch.selection ParamFct    NA    NA       3   <NoDefault[3]>
#>  2:     encode.affect_columns ParamUty    NA    NA     Inf    <Selector[1]>
#>  3:             encode.method ParamFct    NA    NA       5   <NoDefault[3]>
#>  4: imputehist.affect_columns ParamUty    NA    NA     Inf   <NoDefault[3]>
#>  5:             kknn.distance ParamDbl     0   Inf     Inf                2
#> ---                                                                        
#> 59:                    svm.nu ParamDbl  -Inf   Inf     Inf              0.5
#> 60:                 svm.scale ParamUty    NA    NA     Inf             TRUE
#> 61:             svm.shrinking ParamLgl    NA    NA       2             TRUE
#> 62:             svm.tolerance ParamDbl     0   Inf     Inf            0.001
#> 63:                  svm.type ParamFct    NA    NA       2 C-classification
#>      parents            value
#>  1:                       knn
#>  2:                          
#>  3:                   one-hot
#>  4:                          
#>  5:                          
#> ---                          
#> 59: svm.type                 
#> 60:                          
#> 61:                          
#> 62:                          
#> 63:          C-classification

可见，所有超参数都多了学习器或管道名字前缀，比如 kknn.k 是KNN 学习器的邻居数参数 k。

嵌套重抽样超参数调参，与前文语法一样，为了加速计算，启动并行：

future::plan("multicore")

设置搜索空间，用 tune_nested() 做嵌套调参：

search_space = ps(
  branch.selection = p_fct(c("kknn", "svm", "ranger")),
  kknn.k = p_int(3, 50, logscale = TRUE,
                 depends = branch.selection == "kknn"),
  svm.cost = p_dbl(-1, 1, trafo = \(x) 10^x,
                   depends = branch.selection == "svm"),
  ranger.mtry = p_int(1, 8,
                      depends = branch.selection == "ranger")
)
rr = tune_nested(
  tuner = tnr("random_search"),
  task = task,
  learner = glearner,
  inner_resampling = rsmp("cv", folds = 3),
  outer_resampling = rsmp("cv", folds = 4),
  measure = msr("classif.ce"),
  term_evals = 10
)

查看结果：

rr$aggregate()    # 总的平均模型性能
#> classif.ce 
#>   0.296875
rr$score()        # 外层 4 次迭代每次的模型性能
#>    task_id
#> 1:    pima
#> 2:    pima
#> 3:    pima
#> 4:    pima
#>                                                                                      learner_id
#> 1: imputehist.missind.featureunion.encode.removeconstants.branch.kknn.svm.ranger.unbranch.tuned
#> 2: imputehist.missind.featureunion.encode.removeconstants.branch.kknn.svm.ranger.unbranch.tuned
#> 3: imputehist.missind.featureunion.encode.removeconstants.branch.kknn.svm.ranger.unbranch.tuned
#> 4: imputehist.missind.featureunion.encode.removeconstants.branch.kknn.svm.ranger.unbranch.tuned
#>    resampling_id iteration classif.ce
#> 1:            cv         1  0.3854167
#> 2:            cv         2  0.2239583
#> 3:            cv         3  0.3020833
#> 4:            cv         4  0.2760417
#> Hidden columns: task, learner, resampling, prediction

6 特征选择

当数据集包含很多特征时，只提取最重要的部分特征来建模，称为特征选择。特征选择可以增强模型的解释性、加速学习过程、改进学习器性能。

常用的特征选择方法有两种：过滤法、包装法。另外，有些学习器内部提供了选择有助于做预测的特征子集的方法，称为是嵌入法。

6.1 过滤法

过滤法，基于某种衡量特征重要度的指标（如相关系数），用外部算法计算变量的排名，只选用排名靠前的若干特征，用 mlr3filters 包实现。

6.1.1 基于重要度指标

过滤法给每个特征计算一个重要度指标值，基于此可以对特征进行排序，然后就可以选出特征子集。

task = tsk("sonar")
filter = flt("auc")
as.data.table(filter$calculate(task))
#>     feature       score
#>  1:     V11 0.281136807
#>  2:     V12 0.242918176
#>  3:     V10 0.232701774
#>  4:     V49 0.231262190
#>  5:      V9 0.230844246
#> ---                    
#> 56:     V60 0.012213244
#> 57:     V30 0.006965729
#> 58:     V57 0.004876010
#> 59:     V55 0.003204235
#> 60:     V40 0.002182595

6.1.2 基于学习器的变量重要度

有些学习器可以计算变量重要度，特别是基于树的模型，目前支持：

“classif.featureless”，“regr.featureless”
“classif.ranger”，“regr.ranger”
“classif.rpart”，“regr.rpart”
“classif.xgboost”，“regr.xgboost”

有些学习器需要在创建时” 激活” 其变量重要性度量。例如，通过 ranger 包来使用随机森林的 ”impurity” 度量：

task = tsk("iris")
learner = lrn("classif.ranger", importance = "impurity")
filter = flt("importance", learner = learner)
filter$calculate(task)
as.data.table(filter)
#>         feature     score
#> 1:  Petal.Width 45.511305
#> 2: Petal.Length 41.987469
#> 3: Sepal.Length  9.381471
#> 4:  Sepal.Width  2.361094

使用上述特征选择可以对特征得分可视化，根据肘法确定保留特征数，然后用 task$select() 选择特征；也可以直接通过管道连接学习器构建图学习器：

task = tsk("spam")
graph = po("filter", filter = flt("auc"), filter.frac = .5) %>>%
  po("learner", lrn("classif.rpart"))
graph$plot()

learner = as_learner(graph)
rr = resample(task, learner, rsmp("cv", folds = 5))
#> INFO  [16:44:45.127] [mlr3] Applying learner 'auc.classif.rpart' on task 'spam' (iter 1/5)
#> INFO  [16:44:45.310] [mlr3] Applying learner 'auc.classif.rpart' on task 'spam' (iter 2/5)
#> INFO  [16:44:45.502] [mlr3] Applying learner 'auc.classif.rpart' on task 'spam' (iter 3/5)
#> INFO  [16:44:45.717] [mlr3] Applying learner 'auc.classif.rpart' on task 'spam' (iter 4/5)
#> INFO  [16:44:45.906] [mlr3] Applying learner 'auc.classif.rpart' on task 'spam' (iter 5/5)
rr$aggregate()
#> classif.ce 
#>  0.1051952

6.2 包装法

包装法，随机选择部分特征拟合模型并评估模型性能，通过交叉验证找到最佳的特征子集，用 mlr3fselect 包实现。

包装法特征选择，与超参数调参道理完全一样。

6.2.1 独立特征选择

适合传统的机器学习套路：将数据集按留出法重抽样划分为训练集和测试集，在训练集上做内层重抽样，多次“训练集拟合模型 + 验证集评估性能”，根据平均性能选出最优特征子集。

选取任务，划分数据集，将测试集索引设置为留出

task = tsk("pima")
split = partition(task, ratio = .8)
task$set_row_roles(split$test, "holdout")

选择学习器

learner = lrn("classif.rpart")

用 fselect() 对学习器做特征选择

instance = fselect(
  fselector = fs("rfe"),
  task = task,
  learner = learner,
  resampling = rsmp("cv", folds = 4),
  measures = msr("classif.ce"),
  term_evals = 10,
  store_models = TRUE
)

查看特征选择结果：

instance$result  # 最佳特征子集
#>     age glucose insulin mass pedigree pregnant pressure triceps
#> 1: TRUE    TRUE   FALSE TRUE     TRUE    FALSE    FALSE   FALSE
#>                     features classif.ce
#> 1: age,glucose,mass,pedigree  0.2801227

instance$archive  # 特征选择档案
#> <ArchiveFSelect>
#>     age glucose insulin mass pedigree pregnant pressure triceps classif.ce
#> 1: TRUE    TRUE    TRUE TRUE     TRUE     TRUE     TRUE    TRUE       0.29
#> 2: TRUE    TRUE   FALSE TRUE     TRUE    FALSE    FALSE   FALSE       0.28
#>    warnings errors runtime_learners  x_domain              timestamp batch_nr
#> 1:        0      0             0.08 <list[8]> 2023-09-13 16:44:46.68        1
#> 2:        0      0             0.02 <list[8]> 2023-09-13 16:44:47.00        2
#>                     importance
#> 1: 8.0,6.8,5.2,4.8,4.8,2.8,...
#> 2:             4.0,2.5,2.0,1.5

对任务选择特征自己，拟合最终模型

task$select(instance$result_feature_set)
learner$train(task)

6.2.2 自动特征选择

上述独立特征选择有两个不足：

特征选择得到的最优特征子集需要手动更新到任务；
不方便实现嵌套重抽样。

自动特征选择器可以弥补上述不足，AutoFSelector 是将特征选择与学习器封装到一起，能实现自动特征选择的过程，并且可以像其他学习器一样使用。

创建任务、选择学习器

task = tsk("pima")
learner = lrn("classif.rpart")

用 auto_fselector() 创建自动特征选择器，注意：不需要提供任务，其它参数与独立特征选择的 fselect() 基本一样：

afs = auto_fselector(
  fselector = fs("random_search", batch_size = 5),
  learner = lrn("classif.rpart"),
  resampling = rsmp("cv", folds = 4),
  measure = msr("classif.ce"),
  term_evals = 10
)

外层采用 5 折交叉验证重抽样，设置 store_models = TRUE 保存每次的模型：

rr = resample(task, afs, rsmp("cv", folds = 5), store_models = TRUE)

查看结果：

rr$aggregate()  # 总的平均模型性能, 也可以提供其它度量
#> classif.ce 
#>  0.2746796

注：若外层重抽样不想做这么多次，可直接用留出重抽样，或者划分训练集测试集，然后将 afs 当学习器使用。

另外，上述的“自动特征选择+ 外层重抽样”，若改用嵌套特征选择 fselect_nested() 实现，代码会更加简洁：

rr = fselect_nested(
  fselector = fs("random_search", batch_size = 5),
  task = tsk("pima"),
  learner = lrn("classif.rpart"),
  inner_resampling = rsmp("cv", folds = 4),
  outer_resampling = rsmp("cv", folds = 5),
  measure = msr("classif.ce"),
  term_evals = 10
)

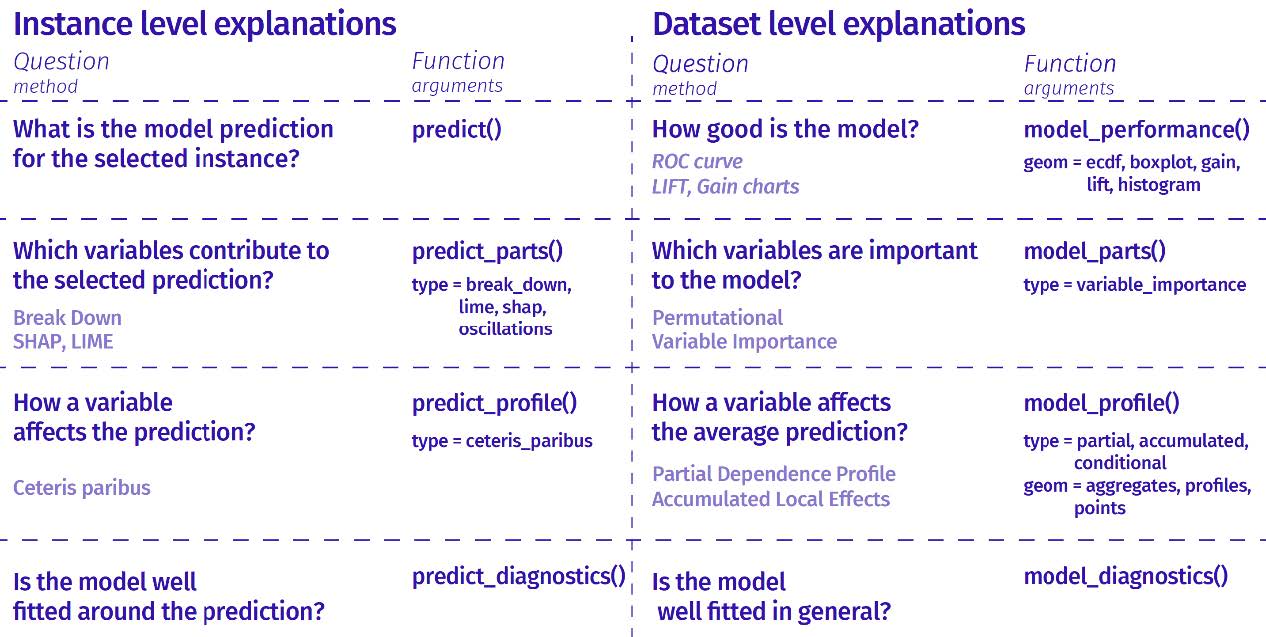
7 模型解释

机器学习模型预测性能强大，但天生不好解释。R 有两个通用框架致力于机器学习模型的解释（支持但不属于 mlr3verse）：iml 包和 DALEX 包。

7.1 iml 包

iml 包提供了分析任何黑盒机器学习模型的工具。

dat = tsk("penguins")$data() %>% na.omit()
task = as_task_classif(dat, target = "species")
learner = lrn("classif.ranger", predict_type = "prob")
learner$train(task)
learner$model
#> Ranger result
#> 
#> Call:
#>  ranger::ranger(dependent.variable.name = task$target_names, data = task$data(),      probability = self$predict_type == "prob", case.weights = task$weights$weight,      num.threads = 1L) 
#> 
#> Type:                             Probability estimation 
#> Number of trees:                  500 
#> Sample size:                      333 
#> Number of independent variables:  7 
#> Mtry:                             2 
#> Target node size:                 10 
#> Variable importance mode:         none 
#> Splitrule:                        gini 
#> OOB prediction error (Brier s.):  0.01793959

iml 包中的所有解释方法都需要机器学习模型和数据封装在 Predictor 对象中。

library(iml)

7.1.1 特征效应

特征效应（FeatureEffects），是计算所有给定特征对模型预测的影响。实现了不同的方法：累积局部效应（ALE）图，部分依赖图（PDP）和个体条件期望（ICE）曲线。

mod = Predictor$new(learner, data = dat, y = "species")
effect = FeatureEffects$new(mod)
effect$plot(features = c("bill_length", "bill_depth",
                         "flipper_length", "body_mass", "year"))

可见，除了年份，所有的特征都提供了有意义的可解释信息。

7.1.2 夏普利值

计算具有夏普利（Shapley）值的单个观测的特征贡献（一种来自合作博弈理论的方法），即单个数据点的特征值是如何影响其预测的。

mod = Predictor$new(learner, data = dat, y = "species")
shapley = Shapley$new(mod, x.interest = dat[1,])
plot(shapley)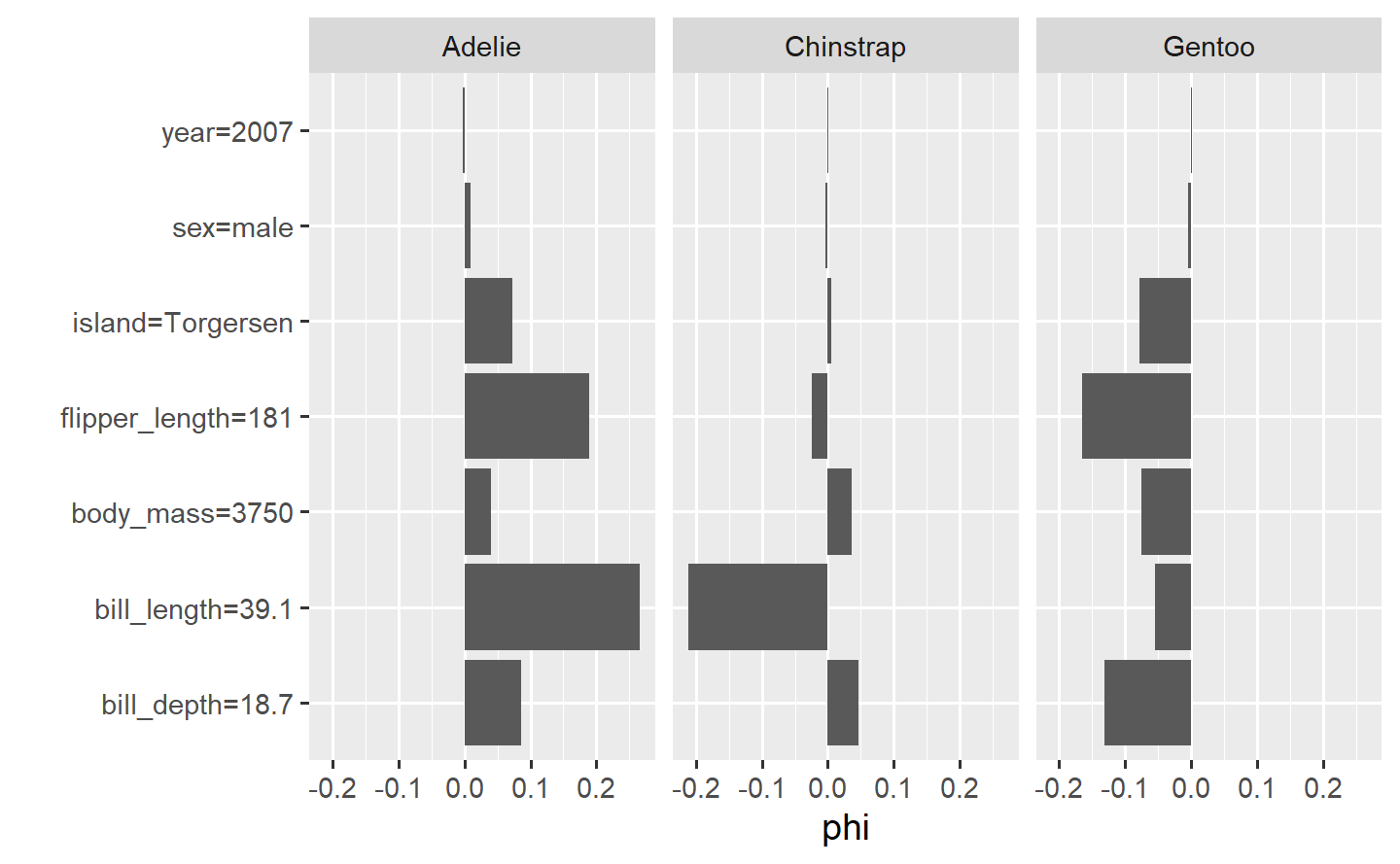

$\phi$值给出了纵轴上数值的概率增加或减少，例如，如果 bill_depth = 18.7，那么一只企鹅是 Gentoo 企鹅的可能性就比较小，而是 Adelie 企鹅的可能性则比 Chinstrap 企鹅大得多。

7.1.3 特征重要度

根据特征重排后模型的预测误差的增量，计算特征的重要度。

mod = Predictor$new(learner, data = dat, y = "species")
imp = FeatureImp$new(mod, loss = "ce")
imp$plot(features = c("bill_length", "bill_depth",
                      "flipper_length", "body_mass", "year"))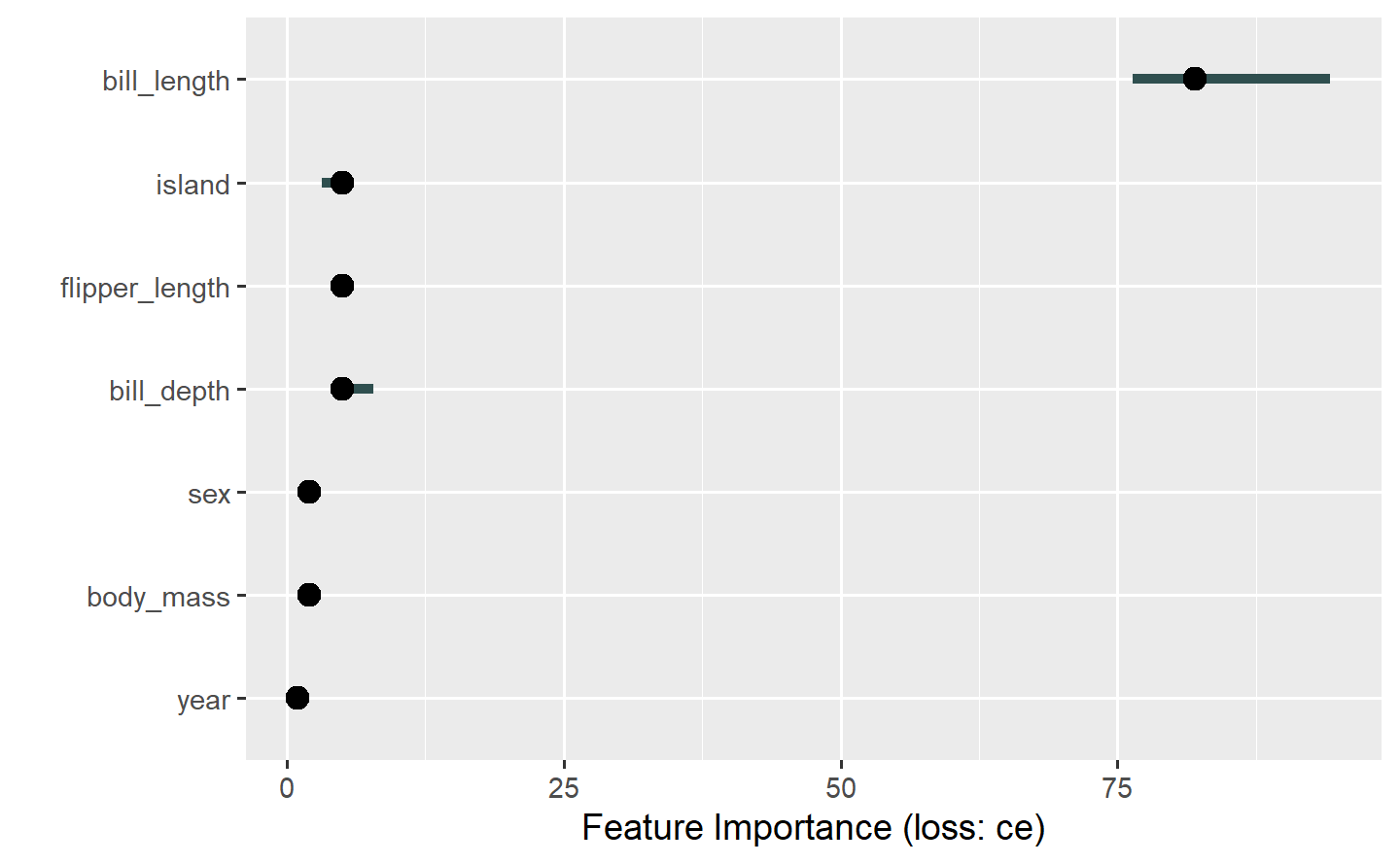

可见，bill_length 具有很高的特征重要度。

注：以上模型解释也可以分别在训练集和测试集上来做，以看对比效果。

7.2 DALEX 包

DALEX 包可以透视任何模型并帮助探索和解释其行为，用各种方法帮助理解输入变量和模型输出之间的联系，有助于在单个观测以及整个数据特征的层面上解释模型。所有的模型解释器都是与模型无关的，可以在不同的模型之间进行比较。该包是 “DrWhy.AI” 可视化模型解释系列包的基石。

以 fifa 数据，预测球员价值 value_eur 为例。

library(DALEX)
library(DALEXtra)
fifa[, c("nationality", "overall", "potential", "wage_eur")] = NULL
fifa = fifa %>% mutate(across(everything(), .fns = as.numeric))

创建任务，选择包含 250 棵决策树的随机森林学习器，训练模型：

task = as_task_regr(fifa, target = "value_eur")
ranger = lrn("regr.ranger", num.trees = 250)
ranger$train(task)
ranger$model
#> Ranger result
#> 
#> Call:
#>  ranger::ranger(dependent.variable.name = task$target_names, data = task$data(),      case.weights = task$weights$weight, num.threads = 1L, num.trees = 250L) 
#> 
#> Type:                             Regression 
#> Number of trees:                  250 
#> Sample size:                      5000 
#> Number of independent variables:  37 
#> Mtry:                             6 
#> Target node size:                 5 
#> Variable importance mode:         none 
#> Splitrule:                        variance 
#> OOB prediction error (MSE):       1.048416e+13 
#> R squared (OOB):                  0.8666863

在开始解释模型行为之前，先创建一个解释器：

ranger_exp = explain_mlr3(ranger, data = fifa, y = fifa$value_eur,
                          label = "Ranger RF")
#> Preparation of a new explainer is initiated
#>   -> model label       :  Ranger RF 
#>   -> data              :  5000  rows  38  cols 
#>   -> target variable   :  5000  values 
#>   -> predict function  :  yhat.LearnerRegr  will be used (  default  )
#>   -> predicted values  :  No value for predict function target column. (  default  )
#>   -> model_info        :  package mlr3 , ver. 0.16.1 , task regression (  default  ) 
#>   -> predicted values  :  numerical, min =  452214 , mean =  7473663 , max =  88491700  
#>   -> residual function :  difference between y and yhat (  default  )
#>   -> residuals         :  numerical, min =  -7777793 , mean =  -375.8719 , max =  17675900  
#>   A new explainer has been created!

7.2.1 特征层面的解释

model_parts() 函数基于排列组合的重要度来计算变量的重要度：

fifa_vi = model_parts(ranger_exp)
head(fifa_vi)
#>              variable mean_dropout_loss     label
#> 1        _full_model_           1334872 Ranger RF
#> 2           value_eur           1334872 Ranger RF
#> 3    movement_balance           1397653 Ranger RF
#> 4           weight_kg           1398740 Ranger RF
#> 5 goalkeeping_kicking           1405245 Ranger RF
#> 6           height_cm           1412798 Ranger RF

plot(fifa_vi, max_vars = 12, show_boxplots = FALSE)

一旦知道了哪些变量是最重要的，就可以使用部分依赖图来显示模型（平均而言）如何随着选定变量的变化而变化。在本例中，它们显示了特定变量和球员价值之间的平均关系。

vars = c("age", "movement_reactions", "skill_ball_control", "skill_dribbling")
fifa_pd = model_profile(ranger_exp, variables = vars)$agr_profiles
fifa_pd
#> Top profiles    : 
#>              _vname_   _label_ _x_  _yhat_ _ids_
#> 1 skill_ball_control Ranger RF   5 7175057     0
#> 2    skill_dribbling Ranger RF   7 7750317     0
#> 3    skill_dribbling Ranger RF  11 7735097     0
#> 4    skill_dribbling Ranger RF  12 7734165     0
#> 5    skill_dribbling Ranger RF  13 7732068     0
#> 6    skill_dribbling Ranger RF  14 7730236     0

plot(fifa_pd)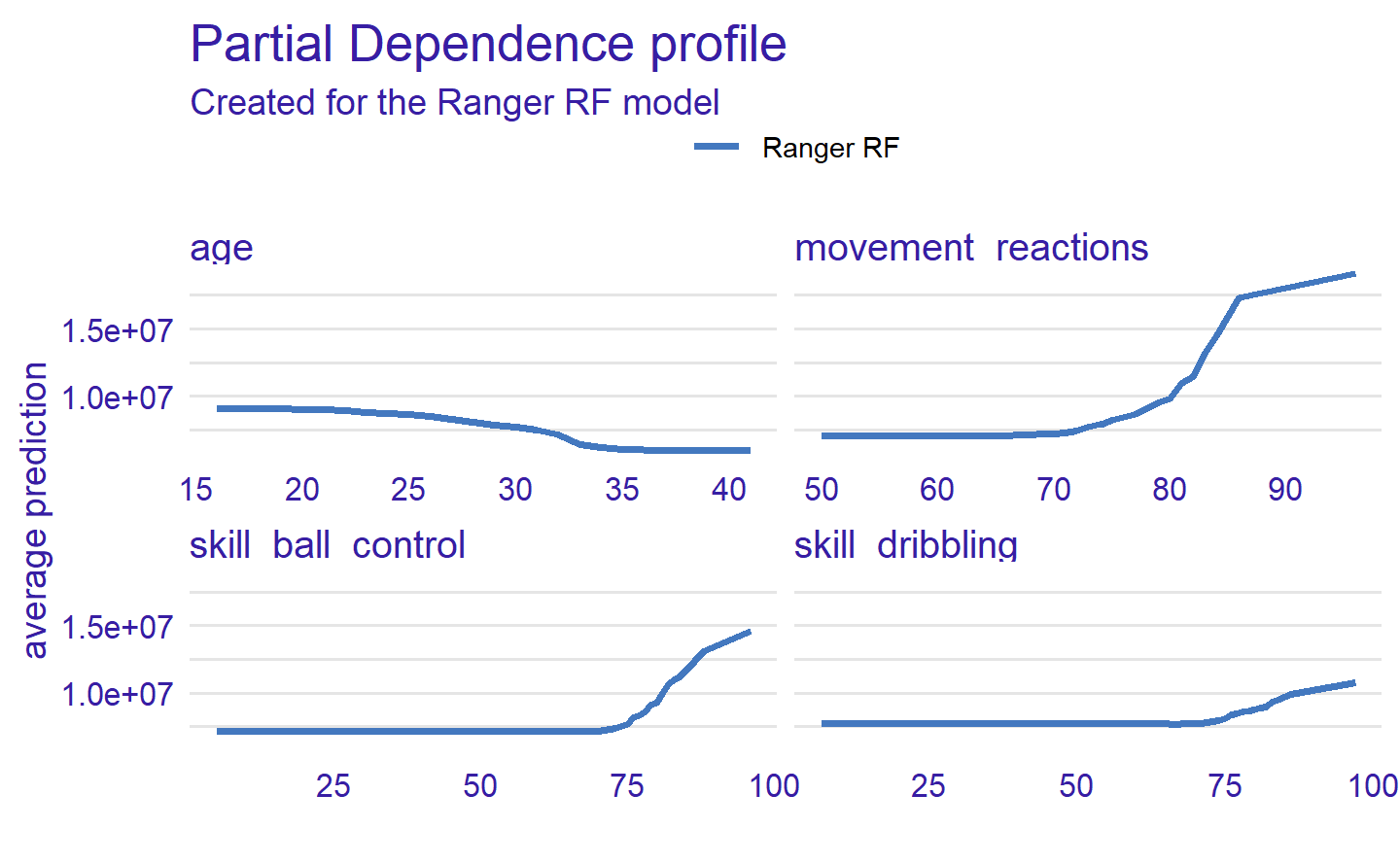

可见，大多数球员特征的一般趋势是相同的。技能越高，球员的价值就越高，只有一个变量例外——年龄。

7.2.2 观测层面的解释

探索模型在单个观测/球员身上的表现，下面以 Cristiano Ronaldo 为例。

ronaldo = fifa["Cristiano Ronaldo", ]
ronaldo_bd = predict_parts(ranger_exp, new_observation = ronaldo)
head(ronaldo_bd)
#>                                       contribution
#> Ranger RF: intercept                       7473663
#> Ranger RF: movement_reactions = 96        10954295
#> Ranger RF: skill_ball_control = 92         8641092
#> Ranger RF: mentality_positioning = 95      5606252
#> Ranger RF: attacking_finishing = 94        4532342
#> Ranger RF: skill_dribbling = 89            4401913

plot(ronaldo_bd)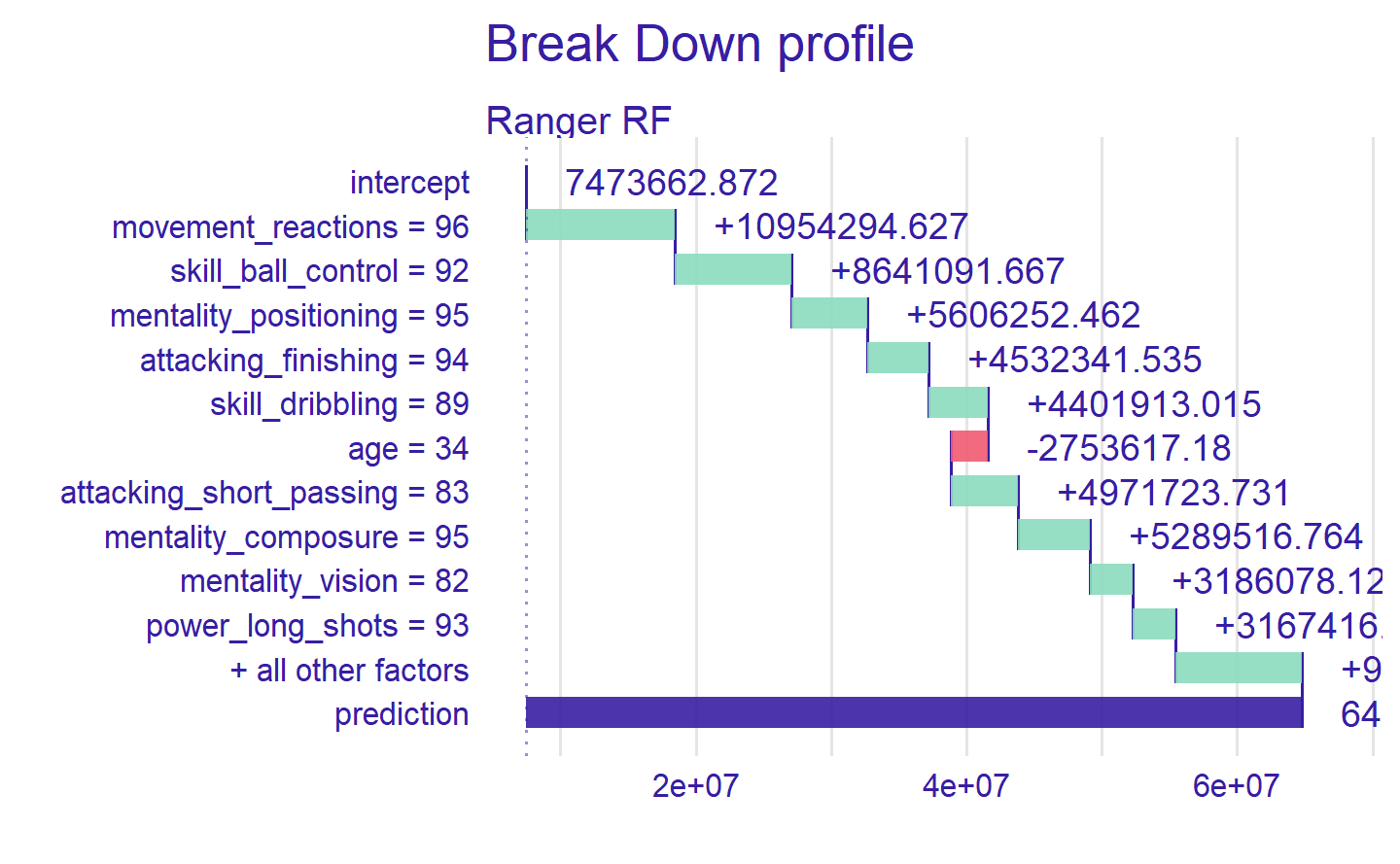

上图展示了各变量对最终预测的贡献估计。Ronaldo 是一名前锋，因此影响他身价的特征是那些与进攻有关的特征，如 attacking_ volleys 或 skill_dribbling。唯一具有负向影响的特征是 age。

检查模型的局部行为的另一种方法是用 SHapley Additive exPlanations（SHAP）。它在局部显示了变量对单一观测的贡献。

ronaldo_shap = predict_parts(ranger_exp, new_observation = ronaldo,
                             type = "shap")
plot(ronaldo_shap)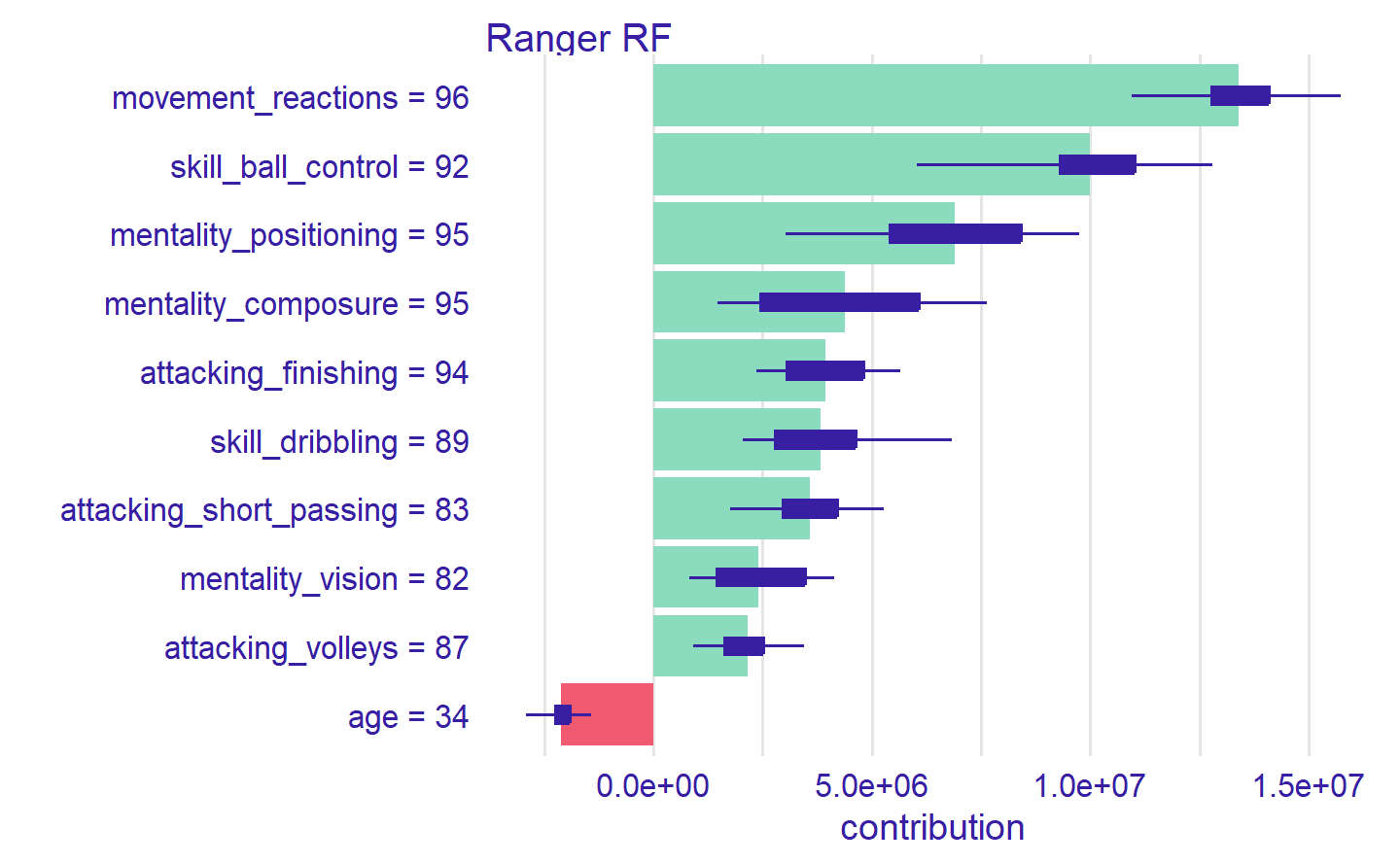

特征效应有部分依赖关系图，对于观测也有相应的版本：Ceteris Paribus。它显示了当只改变一个变量而其他变量保持不变时，模型对观测的反应（蓝点代表原始值）：

ronaldo_cp = predict_profile(ranger_exp, ronaldo, variables = vars)
plot(ronaldo_cp, variables = vars)

更多机器学习模型解释理论方法请参阅 Interpretable Machine Learning: A Guide for Making Black Box Models Explainable.